Question

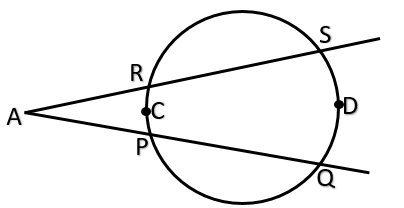
In the following figure, secants containing chords RS aand PQ of a circle intersect each other in point A in the exterior of a circle. If m(arcPCR) = ${{26}^{\circ }}$ and m(arcQDS) = ${{48}^{\circ }}$ then find a measure of arc PQR.

Answer 1

Hint: Now by inscribed angle theorem we have that the angle inscribed is 2 times the measure of the arc. Hence we can form an equation with this condition and then divide the whole equation by 2. Hence we will get the value of the measure of angle PQR.

Complete step-by-step answer:
Now we are given that in the figure RS and PQ intersect each other at A.
We have RS and PQ are secants of the given circle.
Now let us join the point Q and point R.

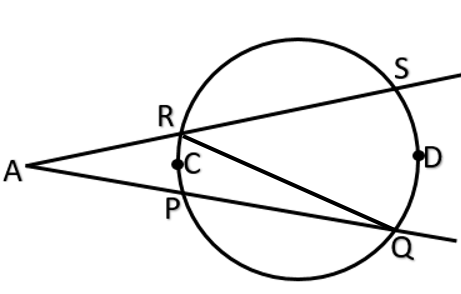
Now we know that P, Q and R are the points lying on the circle.
Now by the inscribed angle theorem we have that the inscribed angle PQR is 2 times the measure of arc.
Now using this property we have $m\left( arcPCR \right)=2\angle PQR$
Now we know that the measure of arc PCR is given as ${{26}^{\circ }}$ .
Hence substituting this value in the above equation we get, \[{{26}^{\circ }}=2\angle PQR\] .
Now dividing the whole equation by 2 we get,
${{\left( \dfrac{26}{2} \right)}^{\circ }}=\angle PQR$ .
Hence we get the value of $\angle PQR$ = ${{13}^{\circ }}$ .

Note: Now note that the measure of arc is nothing but measure of angle made by the point at the center of the circle. Hence we can also say that the angle inscribed is twice the central angle. Now the angle inscribed by the endpoints of the arc is always the same if the endpoints are the same. Also the angle inscribed by the endpoint of diameter is always equal to ${{90}^{\circ }}$ .