Question

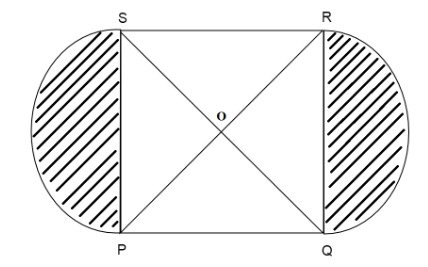
In the following figure, PQRS is square lawn with side \[PQ = 42\] meters. Two semicircular flower beds are there on the sides PS and QR with center at O, the intersections of its diagonals. Find the total area of the two flower beds(shaded part).

Answer 1

Hint: Here we take the side of the square as diameter of the semicircle and find the radius. Find the area of semicircular flower beds by dividing the area of the circle by 2. Multiply the area of one semicircular flower bed into a number of flower beds to obtain the total area covered by flower beds.
* A semicircle is half part of the circle. Radius of the semicircle is the same as the radius of the circle. Area of the semicircle is half of the area of the circle.
* Area of semicircle \[ = \dfrac{1}{2}\pi {r^2}\]
* Diameter of a circle is twice the length of the radius of the circle.

Complete step-by-step answer:
We know PQRS is a square.
\[ \Rightarrow \]Sides of a square are equal in length.
\[ \Rightarrow PQ = QR = RS = SP\]
We are given the length of side\[PQ = 42\]meters
\[ \Rightarrow QR = 42\]meters, \[SP = 42\]meters
So, the diameters of both semicircles are the same i.e. 42 meters.
We find the radius of the semicircles by dividing the diameter by 2
Radius of semicircles with diameter 42 meters \[ = \left( {\dfrac{{42}}{2}} \right)\]meters
\[ \Rightarrow \]Radius of semicircles \[ = 21\]meters
Since the two semicircles have the same radius, then the two semicircles will have the same area.
Area of a circle with radius ‘r’ is given by \[\pi {r^2}\]
\[ \Rightarrow \]Area of semicircle with radius ‘r’ \[ = \dfrac{{\pi {r^2}}}{2}\]
Substitute the value of radius as 21.
\[ \Rightarrow \]Area of semicircle with radius 21 \[ = \dfrac{{\pi {{(21)}^2}}}{2}\]
Open the square of value in numerator
\[ \Rightarrow \]Area of semicircle\[ = \pi \times \dfrac{{21 \times 21}}{2}\]
Substitute the value of \[\pi = \dfrac{{22}}{7}\]
\[ \Rightarrow \]Area of semicircle\[ = \dfrac{{22}}{7} \times \dfrac{{21 \times 21}}{2}\]
Write factors of the numbers 22 and 21
\[ \Rightarrow \]Area of semicircle\[ = \dfrac{{2 \times 11}}{7} \times \dfrac{{3 \times 7 \times 3 \times 7}}{2}\]
Cancel the same factors from numerator and denominator.
\[ \Rightarrow \]Area of semicircle\[ = 11 \times 3 \times 3 \times 7\]
\[ \Rightarrow \]Area of semicircle\[ = 693\] square meters
So, we have two semicircles with the same area.
\[ \Rightarrow \]Area of two semicircles\[ = 693 \times 2\] square meters
\[ \Rightarrow \]Area of two semicircles\[ = 1386\]square meters

So, the area of the shaded region is 1386 square meters.

Note: Students might make the mistake of writing the final answer as the total area as we are also given a square with length of its side. Keep in mind the shaded region is only the semicircular part on both sides. Also, many students might try to find the diagonals of the triangles formed and then draw altitude and then find the radius of the semicircle. This is an unnecessary long process. Always write the SI units of area in square terms along with the value of area and SI unit of length along with length.