Question

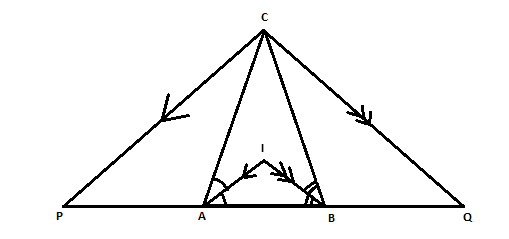
In the following figure; IA and IB are bisectors of angles CAB and CBA respectively CP is parallel to IA and CQ is parallel to IB.
Hence,
PQ = the perimeter of the triangle $\vartriangle $ABC.
State whether the above statement is true or false.
 

A. True
B. False

Answer 1

Hint: Based on the properties of triangle and transversal of parallel lines we can prove that PQ is the perimeter of the $\vartriangle $ABC. When a transversal intersects parallel lines, many angles are congruent. Here PQ is the transversal for parallel lines CP, IA and CQ, IB.

Complete step by step answer:
Given:
IA bisects $\angle CAB$
IB bisects $\angle CBA$
CP is parallel to IA and CQ is parallel to IB.
The angle bisector of an angle of a triangle is a straight line that divides the angle into two congruent angles.

$\angle CAI = \angle IAB$… (1) (IA is given as an angle bisector)
Also, $\angle CPA = \angle IAB$… (2) (Corresponding angles for parallel lines PC and IA)
And,$\angle CAB = \angle CPA + \angle ACP$ (Exterior angle property)
$\angle CAI + \angle IAB = \angle CPA + \angle ACP$
$\angle CAI = \angle ACP$… (3)
Hence (1), (2), (3)
$\angle CPA = \angle PCA = \angle CAI = \angle IAB$ … (4)
Similarly, we can say that,
$\angle CBI = \angle IBA = \angle BCQ = \angle BQC$ … (5)

Now, In Triangle $\vartriangle $CPA
$\angle CPA = \angle PCA$ … [From (4)]
Hence, AC = AP … (6) [Since, sides opposite to equal angles are also equal]

Also, consider triangle $\vartriangle $BCQ
$\angle BCQ = \angle BQC$
Hence, BC = BQ … (7) [Since, sides opposite to equal angles are also equal]

Now, PQ = PA + AB + BQ
PQ = AC + AB + BC
PQ = Perimeter of triangle $\vartriangle $ABC … [From (6) and (7)]

Since perimeter of a triangle the sum of all 3 sides of the triangle
$\therefore $PQ = AB + BC + AC = Perimeter of $\vartriangle $ABC

So, the correct answer is “Option A”.

Note: If transversal intersects with two or more parallel lines then the formed corresponding angles, alternate interior angles and alternate exterior angles are congruent. The pairs of consecutive interior angles formed by the transversal are supplementary. The three angle bisectors of the angles of a triangle meet in a single point, called the incenter. And for an equilateral triangle the incenter and the circumcenter will be the same.