Question

In the following figure AP and BP are tangents to the circle and $\angle APB=40{}^\circ $ . Find the value of $\angle AQB$ .

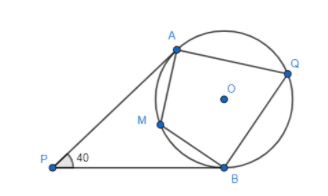
Answer 1

Hint: Start by drawing a representative diagram of the above situation and draw line segments joining AO and BO. Use the property that the angle between radius and tangent of a circle is always $90{}^\circ $ . So, in quadrilateral AOBP, two angles are right angles and the one is $40{}^\circ $ . Use the property that the sum of all the interior angles of quadrilateral is equal to $360{}^\circ $ and finally use that the angle subtended by a segment of the circle at the centre of the circle is twice the angle subtended by the segment at the circumference of the circle to reach the answer.

Complete step-by-step answer:
Let us start by drawing a representative diagram of the situation mentioned in the question along with required construction.

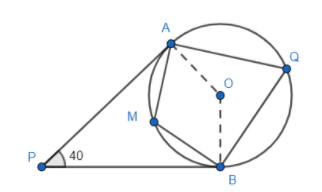
In the above figure, AP and BP are the tangents to the circle with centre O. Now we know that the tangents from a given point P. Angle OAP and angle OBP is $90{}^\circ $ as the angle between radius and tangent of a circle is always $90{}^\circ $ .
Now according to the property that the sum of all the interior angles of a quadrilateral is equal to $360{}^\circ $ . So, if we apply this in quadrilateral AOBP, we get
$\angle APB+\angle OAP+\angle OBP+\angle BOA=360{}^\circ $
\[\Rightarrow 40{}^\circ +90{}^\circ +90{}^\circ +\angle BOA=360{}^\circ \]
\[\Rightarrow \angle BOA=140{}^\circ \]
Now we know that the angle subtended by a segment of the circle at the centre of the circle is twice the angle subtended by the segment at the circumference of the circle.
 \[\therefore \dfrac{1}{2}\times \angle BOA=\angle AQB\]
\[\Rightarrow \dfrac{1}{2}\times 140{}^\circ =70{}^\circ =\angle AQB\]
Therefore, the value of \[\angle AQB=70{}^\circ \] .

Note: Remember that AMBQ is a cyclic quadrilateral, so if needed you can use the properties of cyclic quadrilateral as well. Also, be very careful while using the relation \[\dfrac{1}{2}\times \angle BOA=\angle AQB\] , because it is a general mistake that students take \[\angle BOA=\dfrac{1}{2}\times \angle AQB\] , which is completely wrong.