Question

In the following figure, $ABCD$ is a cyclic quadrilateral in which $AD$ is parallel to $BC$.

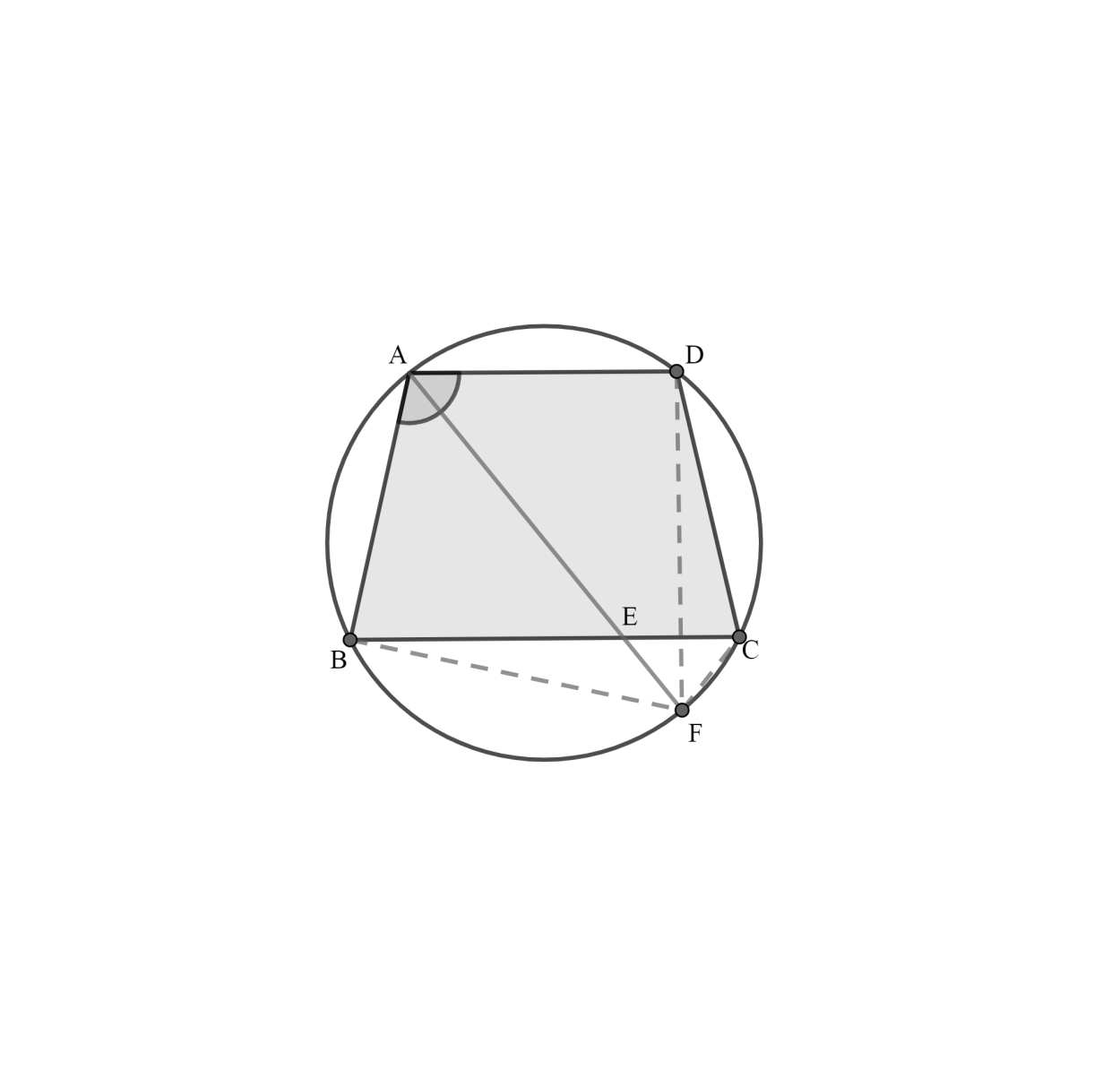
If the bisector of angle $A$ meets $BC$ at point $E$ and the given circle at point $F$ , prove that:
A. $EF=FC$
B. $BF=DF$

Answer 1

Hint:We will prove the given two statements by using different properties of the cyclic quadrilaterals that are opposite angles have the sum equal to ${{180}^{\circ }}$ and also the sum of angles of a triangle is ${{180}^{\circ }}$and then we will apply the property for angles subtended by equal arcs.

Complete step by step answer:
It is given that bisector of angle $A$ meets $BC$ at point $E$ and the given circle at point $F$ , $DF$ and $BF$ are then joined,
We will now take the first option and we have to prove: $EF=FC$
So, it is given that $AD\parallel BC$ , now since $AF$ is the bisector of angle $A$ .
Therefore, $\angle BAF=\angle DAF$ and also $\angle DAE=\angle BAE$ . Now, we know that the alternate angles between two parallel lines are equal, therefore: $\angle DAE=\angle AEB$. This implies that $\angle BAE=\angle AEB$
Now in $\Delta ABE$ , we know that sum of angles in a triangle is ${{180}^{\circ }}$ $\angle ABE+\angle AEB+\angle BAE={{180}^{\circ }}\Rightarrow \angle ABE={{180}^{\circ }}-2\angle AEB$ ,
Now, $\angle ABE=\angle ABC={{180}^{\circ }}-2\angle AEB\text{ }.............\text{Equation 1}$
We now know that vertically opposite angles are equal therefore,
$\angle AEB=\angle CEF\text{ }..........\text{Equation 2}$ .
Now, we know that the sum of opposite angles in a cyclic quadrilateral is ${{180}^{\circ }}$ , therefore:
$\angle ADC+\angle ABC={{180}^{\circ }}\Rightarrow \angle ADC={{180}^{\circ }}-\angle ABC$ , now we will put the value of $\angle ABC$ from equation 1:
\[\begin{align}
  & \Rightarrow \angle ADC={{180}^{\circ }}-\left( {{180}^{\circ }}-2\angle AEB \right) \\
 & \Rightarrow \angle ADC=2\angle AEB\text{ }.............\text{Equation 3} \\
\end{align}\]
Similarly,
$\angle ADC+\angle AFC={{180}^{\circ }}\Rightarrow \angle AFC={{180}^{\circ }}-\angle ADC$ , now we will put the value of $\angle ADC$ from equation 3:
\[\begin{align}
  & \Rightarrow \angle AFC={{180}^{\circ }}-\left( 2\angle AEB \right) \\
 & \Rightarrow \angle AFC={{180}^{\circ }}-2\angle AEB\text{ }............\text{Equation 4} \\
\end{align}\]
Now in $\Delta ECF$ , we know that sum of angles in a triangle is ${{180}^{\circ }}$ , we will put the value from equation 2 and equation 4:
$\angle ECF+\angle AFC+\angle CEF={{180}^{\circ }}\Rightarrow \angle ECF={{180}^{\circ }}-\left( \angle AFC+\angle CEF \right)$,
Now:
$\begin{align}
  & \Rightarrow \angle ECF={{180}^{\circ }}-\left( {{180}^{\circ }}-2\angle AEB+\angle AEB \right) \\
 & \Rightarrow \angle ECF=\angle AEB\text{ }..........\text{Equation 5} \\
\end{align}$
Now, from equation 2 and equation 5 , we have: $\angle ECF=\angle CEF$ , therefore: $EF=FC$ .
Hence Proved.
Now, we will consider part B that is: $BF=DF$ , now we know that: $\angle BAF=\angle DAF$ , why $\angle BAF$ is subtended by arc $BF$ and $\angle DAF$ is subtended by arc $DF$.
So, equal angles are subtended by equal arcs and equal arcs subtend equal chords, therefore: $BF=DF$.
Hence proved.

Note:
 Always try and explain each and every step as while proving some statements as it will be better for the understanding of examiner. Always be careful while analyzing the figure because it will help us in solving the question. Also be careful with the signs in the equations for example in: $\angle ECF={{180}^{\circ }}-\left( {{180}^{\circ }}-2\angle AEB+\angle AEB \right)$ , if we make the mistake of even one sign let’s say: \[\angle ECF={{180}^{\circ }}-\left( {{180}^{\circ }}-2\angle AEB-\angle AEB \right)\] then instead of $\angle ECF=\angle AEB\text{ }$ we would get: $\angle ECF=3\angle AEB\text{ }$