Question

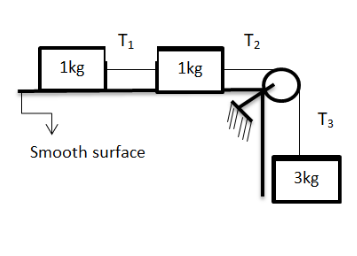
In the following diagram find value of \[{T_2}\].

A. $12N$
B. $6N$
C. $4N$
D. $1N$

Answer 1

Hint:The tension acting on \[{T_2}\] and\[{T_3}\] can be considered to be almost the same. This is because they are acted upon by the same mass pulling the strings downwards. Also, the motion of masses on the surface will almost be the same due to the hanging mass.
Tension on the strings can be derived by considering the equation of motion of masses.

Formula Used:
The tension in the string is given by the formula: \[{T_2} = \dfrac{{({m_1} + {m_2}){m_3}}}{{({m_1} + {m_2}) + {m_3}}}g\]

Complete step by step answer:
The force exerted through a thread, rope, chain or any stretched string is called tension. The direction of tension is so as to pull the body. As seen in the given figure, three bodies of masses 1kg, 1kg and 3kg are given. Consider the names for the masses are \[{m_1},{m_2}\] and \[{m_3}\] respectively such that \[{m_3}\] is the mass of 3kg. Tension \[{T_1}\] ,\[{T_2}\] and \[{T_3}\] are the tension on the string that connects the masses.
Then, equation of motion of mass \[{m_1}\] and \[{m_2}\] will be as follows
\[T = \left( {{m_1} + {m_2}} \right)a\]\[ \to (1)\]
where, \[T\] is the tension produced in the string\[{T_1}\] and \[{T_2}\]and\[a\] is the acceleration produced due to this tension.
On the other hand, equation of motion of mass \[{m_3}\] will be as follows:
\[{m_3}g - T = {m_3}a\]
Here, \[{T_{}}\] is the tension in \[{T_3}\] part of the string.
The acceleration can be written as
\[a = \dfrac{{{m_3}g}}{{({m_1} + {m_2}) + {m_3}}}\]
And, thus tension \[{T_2}\] will be
\[{T_2} = \dfrac{{({m_1} + {m_2}){m_3}}}{{({m_1} + {m_2}) + {m_3}}}g\]
\[\therefore {T_2} = \dfrac{{(1 + 1) \times 3}}{{(1 + 1) + 3}} \times 10 = \dfrac{{60}}{5} = 12N\]

Hence, option (A) is the correct answer.

Note: Here \[g\] is approximated to 10 meters per seconds squared. Students must also note that the two blocks of masses are resting on a smooth surface. Therefore, there will be no frictional force between the two blocks and the surface.