Question

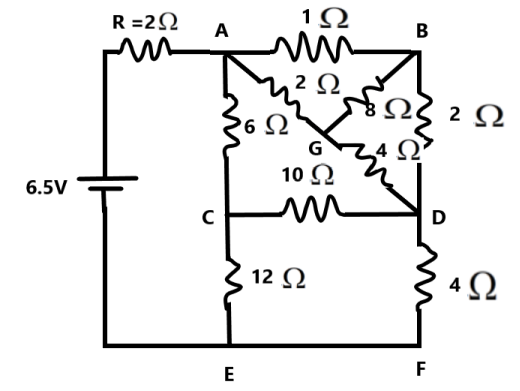
In the following circuit, the current through the resistor R (\[=2\Omega \]) is I amperes. Find the value of I.

Answer 1

Hint: We need to find the current through a specific resistance in the given circuit. We need to find the equivalent resistance of the complete circuit and understand the current flowing through one of the resistances. We can use different methods to approach this situation.

Complete step by step answer:
We can find the current flowing through the resistor on finding the equivalent resistance of the circuit. The portion ABDFECA is in series with the resistor R. We can find the resistance of the wing ABDFECA.

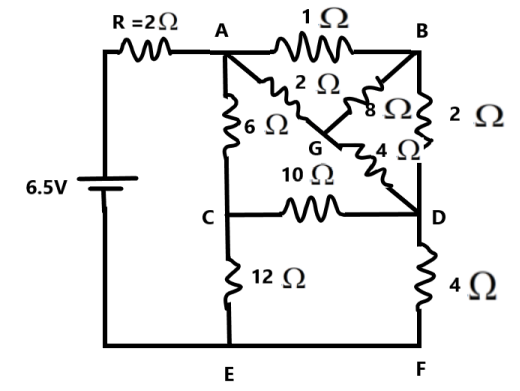
Let us consider the circuit ABDGA, we understand that the nodes B and G are in equipotential condition, therefore there is no current through the \[8\Omega \] resistor. This is in accordance with Wheatstone's bridge condition. The ratio of the resistors across BG is equal.
The resistance of the part ABDGA is given as –
\[\begin{align}
  & {{R}_{ABD}}=1+2=3\Omega \\
 & {{R}_{AGD}}=2+4=6\Omega \\
 & \Rightarrow \dfrac{1}{{{R}_{ABDGA}}}=\dfrac{1}{{{R}_{1}}}=\dfrac{1}{{{R}_{ABD}}}+\dfrac{1}{{{R}_{AGB}}} \\
 & \Rightarrow \dfrac{1}{{{R}_{1}}}=\dfrac{1}{3}+\dfrac{1}{6} \\
 & \therefore {{R}_{1}}=2\Omega \\
\end{align}\]
The circuit simplifies as shown in the figure below.

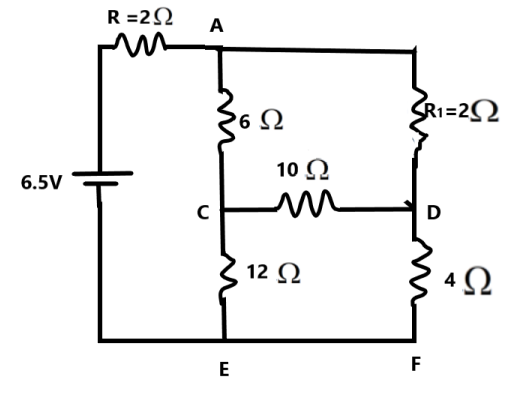
We understand that the remaining portion is also satisfying the Wheatstone’s condition in the 1:3 ratio. The C and D are equipotential nodes. The \[10\Omega \]resistance doesn’t have any current through it.
The resistance through the ADFECA can be found as –
\[\begin{align}
  & {{R}_{ACE}}=6+12=18\Omega \\
 & {{R}_{ADF}}=2+4=6\Omega \\
 & \Rightarrow \dfrac{1}{{{R}_{ADFECA}}}=\dfrac{1}{{{R}_{2}}}=\dfrac{1}{{{R}_{ACE}}}+\dfrac{1}{{{R}_{ADF}}} \\
 & \Rightarrow \dfrac{1}{{{R}_{2}}}=\dfrac{1}{18}+\dfrac{1}{6} \\
 & \therefore {{R}_{2}}=4.5\Omega \\
\end{align}\]
The circuit simplifies further as –

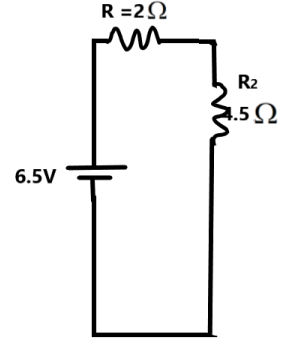
From the above the circuit we get the equivalent resistance as –
\[\begin{align}
  & {{R}_{eq}}={{R}_{2}}+R \\
 & \Rightarrow {{R}_{eq}}=4.5+2 \\
 & \Rightarrow {{R}_{eq}}=6.5\Omega \\
\end{align}\]
Now, we can find the current through the circuit as –
\[\begin{align}
  & I=\dfrac{V}{{{R}_{eq}}} \\
 & \Rightarrow I=\dfrac{6.5}{6.5} \\
 & \therefore I=1A \\
\end{align}\]
The current through the resistor R is also 1A as the two are in series connection.

Note:
The Wheatstone’s bridge condition simplifies the resistance in most of the cases. The condition is used to calibrate the resistances across the equipotential points. The meter bridge and the potentiometer use this condition as the working principle.