Question

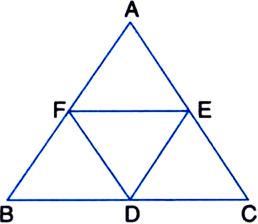
In the figure\[\Delta ABC\] ,\[D,E,F\] are the mid points of the side \[BC,CA\] and \[AB\] respectively. Show that
(i) \[BDEF\] is a parallelogram
(ii) \[ar(\Delta DEF) = \dfrac{1}{4}ar(\Delta ABC)\]
(iii) \[ar(BDEF) = \dfrac{1}{2}ar(\Delta ABC)\]

Answer 1

Hint: Here, we use (i) the properties of congruence of triangles
(ii) properties of parallel lines
(iii) properties of midpoint of a line

Complete step-by-step answer:
Given, triangle in which D,E and F are the mid points of the sides and
(i)to prove that \[BDEF\] is a parallelogram
We know that the line segments joining the mid-point of two sides of a triangle are parallel to the 3rd side.
Now consider \[\Delta ABC\]
Where \[F\] is the mid-point of \[AB\]
and \[E\] Is the mid-point of \[AC\]
Which implies \[EF||BC\]
Which implies \[EF||BD\] (since, parts of the parallel lines are parallel)
Similarly, \[DE||BF\]
Which implies \[BDEF\] is a parallelogram
Hence proved

(ii) to prove \[ar(\Delta DEF) = \dfrac{1}{4}ar(\Delta ABC)\]
Using first part we can prove that \[FDCE\] is a parallelogram and \[AFDE\] is a parallelogram
As we know that the diagonals of a parallelogram divides it into two congruent triangles
Therefore in \[BDEF\]
\[\Delta DBF \cong \Delta DEF\]
It implies \[ar(\Delta DBF) = ar(\Delta DEF)......(1)\] (as area of congruent triangles is same)
Similarly,
\[ar(\Delta DEC) = ar(\Delta DEF)......(2)\]
\[ar(\Delta AFE) = ar(\Delta DEF)......(3)\]
From equation (1), (2) and (3) we get
\[ar(\Delta DBF) = ar(\Delta DEC) = ar(\Delta AFE) = ar(\Delta DEF).\]
Now, \[ar(\Delta DBF) + ar(\Delta AFE) + ar(\Delta DEC) + ar(\Delta DEF) = ar(\Delta ABC)\]
\[ \Rightarrow 4ar(\Delta DEF) = ar(\Delta ABC)\]
\[ \Rightarrow ar(\Delta DEF) = \dfrac{1}{4}ar(\Delta ABC)\]
Hence proved

(iii) to prove \[ar(BDEF) = \dfrac{1}{2}ar(\Delta ABC)\]
We know that \[ar(BDEF) = ar(\Delta DBF) + ar(\Delta DEF)\]
\[ \Rightarrow ar(BDEF) = 2ar(\Delta DEF)\]
\[ \Rightarrow ar(\Delta DEF) = \dfrac{1}{2}ar(BDEF)......(4)\]
Also, \[ar(\Delta DEF) = \dfrac{1}{4}ar(\Delta ABC)......(5)\]
Therefore, from equation (4) and (5) we get
\[ \Rightarrow \dfrac{1}{2}ar(BDEF) = \dfrac{1}{4}ar(\Delta ABC)\]
\[ \Rightarrow ar(BDEF) = \dfrac{1}{2}ar(\Delta ABC)\]
Hence, proved

Note: The above results could only be shown because we could use the properties of the midpoints given in the question. If we hadn’t been given the midpoints the above results could not have been stated.