Question

In the figure, $ XY\parallel AC $ and $ XY $ divides the triangular region $ ABC $ into two equal areas. Determine $ AX:XB. $
(A) $ (\sqrt 3 - 1):1 $
(B) $ (\sqrt 2 - 1):1 $
(C) $ (\sqrt 7 - 1):1 $
(D) $ (\sqrt {11} - 1):1 $

Answer 1

Hint: Prove that the triangles $ \Delta ABC $ and $ \Delta BXY $ are similar. And then use the property that the ratio of area of two similar triangles is equal to the square of the ratio of the corresponding sides of the two triangles. This will help you find the required ratio.

Complete step-by-step answer:
In this question a figure I given as,

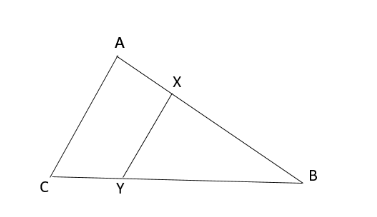
It is given in the question that, $ XY\parallel AC $
 $ XY $ divides the triangular region $ ABC $ into two equal areas.
We have to find the ratio, $ AX:XB. $
Consider the triangles, $ \Delta ABC \& \Delta DXY. $
 $ LB = LB $ . . . . (common side)
 $ \angle BXY = \angle BAC $ (corresponding angles of parallel sides)
 $ \angle BYX = \angle BCC $ . . . . (By corresponding angle properties)
So, by using ASA criteria of similarity of triangles, we can say that
 $ \Delta ABC \sim \Delta BXY $
So by ASA , $ \Delta ABC \sim \Delta BXY $
Now, we know that the ratio of the area of the similar triangles is equal to the square of the ratio of the corresponding sides of the two triangles.
By this property, we can write the ratio of the areas of $ \Delta ABC\& \Delta BXY = $ square of ratio of their proportional sides.
 $ \Rightarrow \dfrac{{Area(\Delta ABC)}}{{Area(\Delta BXY)}} = {\left( {\dfrac{{AB}}{{BX}}} \right)^2} $ . . . . . . . (By similarity properties)
 $ \Rightarrow $ $ \dfrac{{Area(\Delta BXY) + Area(quadrilateral,ACXY)}}{{Area(\Delta BXY)}} = {\left( {\dfrac{{AX}}{{BX}}} \right)^2} $
 $ \Rightarrow \dfrac{{2Area(\Delta BXY)}}{{Area(\Delta BXY)}} = {\left( {\dfrac{{AB}}{{BX}}} \right)^2} $
By cancelling the common terms we can write
  $ \Rightarrow \dfrac{2}{1} = {\left( {\dfrac{{AB}}{{BX}}} \right)^2} $
 $ \Rightarrow \dfrac{{AB}}{{BX}} = \sqrt 2 $
 $ AB = \sqrt 2 BX $ . . . . . (1)
Now we have to find $ \dfrac{{AX}}{{BX}} $
Here, $ AB $ can be written as $ (AB + BX) $ from figure,
 $ \Rightarrow AB = AX + BX $
Substitute in equation (1)
 $ AX + BX = BX\sqrt 2 $
 $ AX = BX\sqrt 2 - BX $
 $ AX = BX\left( {\sqrt 2 - 1} \right) $
 $ \therefore \dfrac{{AX}}{{BX}} = (\sqrt 2 - 1):1 $
So, the correct answer is “Option B”.

Note: XY divides triangle $ ABC $ into two parts of equal area does not mean that $ X and Y $ mid-points of sides $ AB $ and $ BC $ . Be careful that knowing the properties of similar triangles is very important to solve such questions.