Question

In the figure, write down each pair of vertically opposite angles.

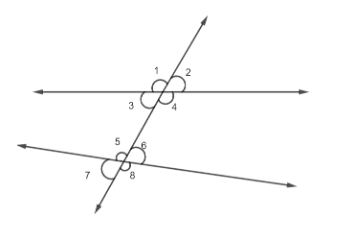
Answer 1

Hint: To solve the given question, we will first find out what vertically opposite angles are. Then we will find the relation between angles 1 and 2 by using the fact that their sum is \[{{180}^{\circ}}\] because they lie on a single line. Then we will find a similar relation between angles 2 and 4. Then we will find a similar relation between angles 4 and 3. Finally, we will find the relation between angles 1 and 4 and angles 2 and 3. If they will be equal, then they will be vertically opposite angles. We will do the same for angles 5, 6, 7 and 8 and obtain vertically opposite angle pairs. Before we solve the question, we must know what vertically opposite angles are. Vertically opposite angles are the angles opposite to each other and are formed when two lines cross. They are always equal.

Complete step-by-step answer:

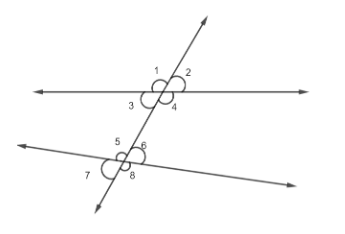
Now, AOB is a straight line, so we have the following relation:
\[\angle 1+\angle 2={{180}^{\circ}}.....\left( i \right)\]
Now POQ is also a straight line, so we will have the following relation:
\[\angle 2+\angle 4={{180}^{\circ}}.....\left( ii \right)\]
Similarly,
\[\angle 3+\angle 4={{180}^{\circ}}.....\left( iii \right)\]
Now, we will subtract (i) from (ii). Thus, we will get,
\[\Rightarrow \left( \angle 2+\angle 4 \right)-\left( \angle 1+\angle 2 \right)={{180}^{\circ}}-{{180}^{\circ}}\]
\[\Rightarrow \angle 4-\angle 1={{0}^{\circ}}\]
\[\Rightarrow \angle 4=\angle 1\]
Now angles 4 and 1 are formed when two lines cross and are equal in magnitude, so they are vertically opposite angles. Now, we will subtract (ii) from (iii). This will give,
\[\Rightarrow \left( \angle 3+\angle 4 \right)-\left( \angle 2+\angle 4 \right)={{180}^{\circ}}-{{180}^{\circ}}\]
\[\Rightarrow \angle 3+\angle 4-\angle 2-\angle 4={{0}^{\circ}}\]
\[\Rightarrow \angle 3-\angle 2={{0}^{\circ}}\]
\[\Rightarrow \angle 3=\angle 2\]
Now, angles 3 and 2 are formed when two lines cross and are equal in magnitude, so they are vertically opposite angles. Similarly, we can say that angles 5 and 8 and angles 6 and 7 are pairs of vertically opposite angles.

Note: Here, we have considered POO’Q, AOB and CO’D are straight lines for finding the vertically opposite angles because the sum of the angles will be \[{{180}^{\circ}}\] only when we will consider that they are straight lines. If they are not straight lines then the pairs we have obtained will not be vertically opposite angles.