Question

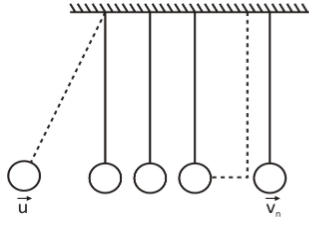
In the figure there are n identical spheres of mass m suspended with wires of equal length. The spheres are almost in contact with each other. Sphere 1 is pulled aside and released . If sphere 1 strikes sphere 2 with velocity u. find an expression for velocity ${v_n}$ of the nth sphere immediately after being struck by the one adjacent to it. The coefficient of restitution for all the impacts is e.
 

Answer 1

Hint: you need to find velocity of sphere after first collision and then find out the relationship between the velocities before and after collision. Once you know the relation you can find the velocity for nth collision.

Complete step by step answer:
let velocities after first collision be ${v_1}$ and ${v_2}$
where${v_1}$is velocity of the first particle and ${v_2}$ is velocity of the second particle.
applying momentum conservation we have
$initial\,momentum = final\,momentum \Rightarrow mu = m{v_1} + m{v_2}$
And $e = \dfrac{{{v_2} - {v_1}}}{u} \Rightarrow eu = {v_2} - {v_1}$
Solving both the equations
$eu = {v_2} - (u - {v_2}) \Rightarrow {v_2} = \dfrac{{(e + 1)u}}{2}$
As we can see velocity changes by a factor of $\dfrac{{e + 1}}{2}$after each collision
So after nth collision velocity will change by a factor of $\dfrac{{{{(e + 1)}^n}}}{{{2^n}}}$
Therefore , ${v_n} = \dfrac{{{{(e + 1)}^n}}}{{{2^n}}}u$

Note:
Although pendulums are colliding but they are colliding in its lowest position(horizontally) so we can treat it as a spheres colliding in plane ground. And if there are multiple collisions on a single sphere we should neglect it unless asked.