Question

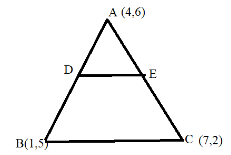
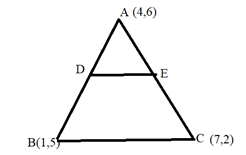
In the figure, the vertices of the \[\Delta ABC\] are \[{\text{A}}\left( {4,6} \right)\], \[B\left( {1,5} \right)\] and \[{\text{C}}\left( {7,2} \right)\] . A line- segment DE is drawn to intersect the sides AB and AC at D and E respectively such that \[\dfrac{{{\text{AD}}}}{{{\text{AB}}}}{\text{ = }}\dfrac{{{\text{AE}}}}{{{\text{AC}}}} = \dfrac{1}{3}\]. Calculate the area of \[\Delta {\text{ADE}}\].

Answer 1

Hint: Here, we will use the Internal section formula which is used for finding the coordinates of a point which divides the line segment into two parts with a particular ratio:

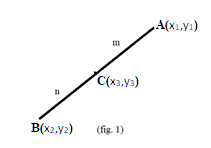
In the above figure (1),
\[{\text{A}}\] and \[{\text{B}}\]are two points having vertices \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\]. \[{\text{C}}\] having vertices \[\left( {{x_3},{y_3}} \right)\] divides the line in a ratio \[m:n\]. So, the formula for finding the vertices of \[{\text{C}}\] is given by the internal section formula which gives:
\[{x_3} = \dfrac{{n{x_1} + m{x_2}}}{{n + m}}\] and \[{y_3} = \dfrac{{n{y_1} + m{y_2}}}{{n + m}}\].
Also, for finding the area of a triangle by using its vertices or determinants we will be using a 3×3 matrix formula which states that for a triangle as drawn below:

\[{\text{Area of triangle}} = \dfrac{1}{2}\left| {\begin{array}{*{20}{l}}
  {{x_1}}&{{y_1}}&1 \\
  {{x_2}}&{{y_2}}&1 \\
  {{x_3}}&{{y_3}}&1
\end{array}} \right|\]
Where, \[\left( {{x_1},{y_1}} \right)\] is the coordinate of the first point of the triangle, \[\left( {{x_2},{y_2}} \right)\] is the coordinate of the second point of the triangle and,\[\left( {{x_3},{y_3}} \right)\] is the coordinate of the third point of the triangle.

Complete step-by-step answer:
Step 1: In the below figure:

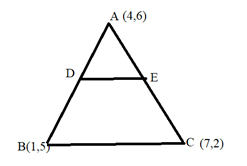
The vertices of point \[{\text{A}}\] and \[{\text{B}}\] in the line segment
\[{\text{AB}}\] are \[\left( {4,6} \right)\] and \[\left( {1,5} \right)\] respectively. Also, we know that, \[\dfrac{{{\text{AD}}}}{{{\text{AB}}}}{\text{ = }}\dfrac{{{\text{AE}}}}{{{\text{AC}}}} = \dfrac{1}{3}\] ( as given in the question).
Now, for calculating the ratio between \[{\text{AD}}\] and
\[{\text{DB}}\], we can write
\[\dfrac{{{\text{AD}}}}{{{\text{AB}}}}{\text{ = }}\dfrac{1}{3}\] as below:
\[ \Rightarrow \dfrac{{{\text{AD}}}}{{{\text{AD}} + {\text{DB}}}} = \dfrac{1}{3}\] ( \[\because \]Point \[{\text{D}}\]divides the line segment \[{\text{AB}}\]into two parts)…. (1)
Step 2:

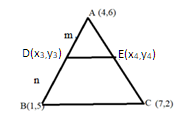
In the above equation (1), by taking
\[3\]into the LHS side and \[{\text{AD}} + {\text{DB}}\] in the RHS side:
\[ \Rightarrow 3{\text{AD}} = {\text{AD}} + {\text{DB}}\]
By taking \[{\text{AD}}\] into the LHS side in the equation \[3{\text{AD}} = {\text{AD}} + {\text{DB}}\], we get:
\[ \Rightarrow 3{\text{AD - AD = DB}}\]
By subtracting the coefficient of \[{\text{AD}}\] we get that in \[3{\text{AD - AD = DB}}\]:
\[ \Rightarrow {\text{2AD = DB}}\]
Now, for finding the ratio between \[{\text{AD}}\] and
\[{\text{DB}}\], we will take \[{\text{DB}}\] into the LHS side and \[2\] into the RHS side in the equation \[{\text{2AD = DB}}\]:
\[ \Rightarrow \dfrac{{{\text{AD}}}}{{{\text{DB}}}} = \dfrac{1}{2}\] …. (2)
From the above equation (2), we can see that the ratio between the \[{\text{AD}}\] and \[{\text{DB}}\] equals to \[\dfrac{1}{2}\], which means that point \[{\text{D}}\] divides the line segment \[{\text{AB}}\] in a ratio of \[1:2\].
Step 3: Similarly, by repeating the step no. 2 for the line segment \[{\text{AC}}\] where \[{\text{E}}\] is a point which divides the line into two parts, we can find the ratio between \[{\text{AE}}\] and \[{\text{EC}}\]. As we have given in the question that, \[\dfrac{{{\text{AE}}}}{{{\text{AC}}}} = \dfrac{1}{3}\], so the ratio will be \[\dfrac{{{\text{AE}}}}{{{\text{EC}}}} = \dfrac{1}{2}\].
\[ \Rightarrow \dfrac{{{\text{AE}}}}{{{\text{EC}}}} = \dfrac{1}{2}\] ………. (3)
Step 4: By taking reference from figure no. (2), for calculating the vertices of \[{\text{D}}\] and \[{\text{E}}\], we will be using the Internal section formula.
First, we will be calculating the vertices of the point \[{\text{D}}\]. Here, we will assume that the vertices of the point \[{\text{D}}\] are \[\left( {{x_3},{y_3}} \right)\].
Now, by substituting the values of vertices of point \[{\text{A(4,6)}}\],
\[{\text{B(1,5)}}\] and \[{\text{D}}\]in the Internal section formula where the ratio is
\[1:2\].
In
\[{x_3} = \dfrac{{n{x_1} + m{x_2}}}{{n + m}}\], where
\[{x_1} = 4\],
\[{x_2} = 1\],\[n = 2\]and \[m = 1\], we get:
\[ \Rightarrow {x_3} = \dfrac{{2 \times 4 + 1 \times 1}}{{2 + 1}}\]
By doing simple multiplication and division in \[{x_3} = \dfrac{{2 \times 4 + 1 \times 1}}{{2 + 1}}\], we get:
\[ \Rightarrow {x_3} = \dfrac{9}{3} = 3\]
For calculating
\[{y_3}\] we will again use the same Internal section formula
\[{y_3} = \dfrac{{n{y_1} + m{y_2}}}{{n + m}}\]:
By putting values in \[{y_3} = \dfrac{{n{y_1} + m{y_2}}}{{n + m}}\], where
\[{y_1} = 6\],\[{y_2} = 5\],\[n = 2\]and \[m = 1\], we get:
\[ \Rightarrow {y_3} = \dfrac{{2 \times 6 + 1 \times 5}}{{2 + 1}}\]
By doing simple multiplication and division in \[{y_3} = \dfrac{{2 \times 6 + 1 \times 5}}{{2 + 1}}\], we get:
\[ \Rightarrow {y_3} = \dfrac{{17}}{3}\]
So, the coordinates of the point \[{\text{D}}\] are \[\left( {3,\dfrac{{17}}{3}} \right)\].
Now, we will be calculating the vertices of the point
\[{\text{E}}\]. Here, we will assume that the vertices of the point \[{\text{E}}\]are \[\left( {{x_4},{y_4}} \right)\].
Thus, by substituting the values of vertices of point
\[{\text{A(4,6)}}\],
\[C(7,2)\] and
\[{\text{E}}\] in the Internal section formula where the ratio is
\[1:2\].
In
\[{x_4} = \dfrac{{n{x_1} + m{x_2}}}{{n + m}}\], where
\[{x_1} = 4\],\[{x_2} = 7\],\[n = 2\]and \[m = 1\], we get:
\[ \Rightarrow {x_4} = \dfrac{{2 \times 4 + 1 \times 7}}{{2 + 1}}\]
By doing simple multiplication and division in \[{x_4} = \dfrac{{2 \times 4 + 1 \times 7}}{{2 + 1}}\], we get:
\[ \Rightarrow {x_4} = \dfrac{{15}}{3} = 5\]
For calculating
\[{y_4}\] we will again use the same Internal section formula
\[{y_4} = \dfrac{{n{y_1} + m{y_2}}}{{n + m}}\]:
By putting values in
\[{y_4} = \dfrac{{n{y_1} + m{y_2}}}{{n + m}}\], where
\[{y_1} = 6\],
\[{y_2} = 2\],\[n = 2\] and \[m = 1\], we get:
\[ \Rightarrow {y_4} = \dfrac{{2 \times 6 + 1 \times 2}}{{2 + 1}}\]
By doing simple multiplication and division in \[{y_4} = \dfrac{{2 \times 6 + 1 \times 2}}{{2 + 1}}\], we get:
\[ \Rightarrow {y_4} = \dfrac{{14}}{3}\]
So, the coordinates of the point \[{\text{E}}\] are \[\left( {5,\dfrac{{14}}{3}} \right)\].
Step 5: Now, we will be calculating the area of
\[\Delta {\text{ADE}}\] having vertices
\[{\text{A}}(4,6)\],
\[{\text{E}}\left( {5,\dfrac{{14}}{3}} \right)\] and
\[{\text{D}}\left( {3,\dfrac{{17}}{3}} \right)\] by using the three by three matrix formula which states that for a triangle where points
\[\left( {{x_1},{y_1}} \right)\], \[\left( {{x_2},{y_2}} \right)\] and \[\left( {{x_3},{y_3}} \right)\] are coordinates of the triangle,
\[{\text{Area of triangle}} = \dfrac{1}{2}\left| {\begin{array}{*{20}{l}}
  {{x_1}}&{{y_1}}&1 \\
  {{x_2}}&{{y_2}}&1 \\
  {{x_3}}&{{y_3}}&1
\end{array}} \right|\].
By substituting the coordinates of points of \[\Delta {\text{ADE}}\] as calculated above in the formula
\[\dfrac{1}{2}\left| {\begin{array}{*{20}{l}}
  {{x_1}}&{{y_1}}&1 \\
  {{x_2}}&{{y_2}}&1 \\
  {{x_3}}&{{y_3}}&1
\end{array}} \right|\] where,
\[{x_1} = 4\],
\[{x_2} = 3\],\[{x_3} = 5\],
\[{y_1} = 6\],\[{y_2} = \dfrac{{17}}{3}\] and \[{y_3} = \dfrac{{14}}{3}\], we get:
\[ \Rightarrow {\text{Area of}}\Delta {\text{ADE = }}\dfrac{1}{2}\left| {\begin{array}{*{20}{l}}
  4&6&1 \\
  3&{\dfrac{{17}}{3}}&1 \\
  5&{\dfrac{{14}}{3}}&1
\end{array}} \right|\]
For calculating the determinant, we will do the multiplication of each term of the first row with the determinant formed by terms which are not in the same row and column of that term and add the result with alternating signs as shown:
\[ \Rightarrow {\text{Area of }}\Delta {\text{ADE = }}\dfrac{1}{2}\left( {4\left| {\begin{array}{*{20}{c}}
  {\dfrac{{17}}{3}}&1 \\
  {\dfrac{{14}}{3}}&1
\end{array}} \right| - 6\left| {\begin{array}{*{20}{c}}
  3&1 \\
  5&1
\end{array}} \right| + 1\left| {\begin{array}{*{20}{c}}
  3&{\dfrac{{17}}{3}} \\
  5&{\dfrac{{14}}{3}}
\end{array}} \right|} \right)\] …………. (4)
Now in the above equation (4), we will solve each determinant by multiplying each element of the first row by diagonally opposite element and subtracting the result:
\[ \Rightarrow {\text{Area of }}\Delta {\text{ADE}} = \dfrac{1}{2}\left( {4\left( {\dfrac{{17}}{3} \times 1 - \dfrac{{14}}{3} \times 1} \right) - 6\left( {3 \times 1 - 1 \times 5} \right) + 1\left( {3 \times \dfrac{{14}}{3} - \dfrac{{17}}{3} \times 5} \right)} \right)\]
Now, by solving the inner brackets:
\[ \Rightarrow {\text{Area of }}\Delta {\text{ADE}} = \dfrac{1}{2}\left( {4\left( {\dfrac{{17}}{3} - \dfrac{{14}}{3}} \right) - 6\left( {3 - 5} \right) + 1\left( {14 - \dfrac{{85}}{3}} \right)} \right)\]
By subtracting the terms inside the brackets:
\[ \Rightarrow {\text{Area of }}\Delta {\text{ADE}} = \dfrac{1}{2}\left( {4\left( 1 \right) - 6\left( { - 2} \right) + 1\left( { - \dfrac{{43}}{3}} \right)} \right)\]
Now, by multiplying the coefficients inside the brackets we get:
\[ \Rightarrow {\text{Area of }}\Delta {\text{ADE}} = \dfrac{1}{2}\left( {4 + 12 - \dfrac{{43}}{3}} \right)\]
Now, by adding the terms inside the brackets we get:
\[ \Rightarrow {\text{Area of }}\Delta {\text{ADE}} = \dfrac{1}{2}\left( {\dfrac{5}{3}} \right)\]
Now finally dividing the term inside the brackets by \[2\]:
\[ \Rightarrow {\text{Area of }}\Delta {\text{ADE}} = \dfrac{5}{6}\]

The area of \[\Delta {\text{ADE}} = \dfrac{5}{6}\].

Note: Students can also solve this problem by using Similarity property, which defines that, if the two sides of a triangle are in the same proportion of the two sides of another triangle, and the angle inscribed by the two sides in both the triangles are equal, then two triangles are said to be similar.

In
\[\Delta {\text{ADE}}\] and \[\Delta {\text{ABC}}\],
\[\dfrac{{{\text{AD}}}}{{{\text{AB}}}}{\text{ = }}\dfrac{{{\text{AE}}}}{{{\text{AC}}}}\;\] (\[\because \]as given in the question)
 We can see that \[\angle {\text{BAC}}\] is common in both the triangles \[\Delta {\text{ADE}}\] and \[\Delta {\text{ABC}}\].
Therefore, \[\Delta {\text{ADE}} {\text{is similar to}} \Delta {\text{ABC}}\] by using SAS (Side -Angle -Side) property of similarity, which states that in any two triangles if the two sides of a triangle are in the same proportion of the two sides of another triangle, and the angle inscribed by the two sides in both the triangles are equal, then two triangles are said to be similar.

\[ \Rightarrow \Delta {\text{ADE}} {\text{is similar to}} \Delta {\text{ABC}}\]
Since \[\Delta {\text{ADE}} {\text{is similar to}} \Delta {\text{ABC}}\] and \[\dfrac{{{\text{AD}}}}{{{\text{AB}}}}{\text{ = }}\dfrac{{{\text{AE}}}}{{{\text{AC}}}} = \dfrac{1}{3}\] so
\[\dfrac{{{\text{Area}}\;\Delta {\text{ADE}}}}{{{\text{Area}}{\text{ }}\Delta {\text{ABC}}}} = \dfrac{1}{9}\], because for two similar triangles, the ratio of their areas is square of the ratio of their corresponding sides.
Now, the area of the
\[\Delta {\text{ABC}}\] is given by the formula
\[\dfrac{1}{2}\left| {\begin{array}{*{20}{l}}
  {{x_1}}&{{y_1}}&1 \\
  {{x_2}}&{{y_2}}&1 \\
  {{x_3}}&{{y_3}}&1
\end{array}} \right|\] where,
\[\left( {{x_1},{y_1}} \right)\],
\[\left( {{x_2},{y_2}} \right)\] and
\[\left( {{x_3},{y_3}} \right)\] are the vertices of the triangle. In this case, we have the coordinates of the points as \[{\text{A}}(4,6)\],\[B(1,5)\]and \[C(7,2)\]. By substituting these values in the formula \[\dfrac{1}{2}\left| {\begin{array}{*{20}{l}}
  {{x_1}}&{{y_1}}&1 \\
  {{x_2}}&{{y_2}}&1 \\
  {{x_3}}&{{y_3}}&1
\end{array}} \right|\],
\[\dfrac{1}{2}\left| {\begin{array}{*{20}{l}}
  4&6&1 \\
  1&5&1 \\
  7&2&1
\end{array}} \right|\] and similarly solving the determinant as we have done in step number 5 we get:
\[ \Rightarrow {\text{Area of }}\Delta {\text{ABC}} = 7.5\]
Since \[\dfrac{{{\text{Area}}\Delta {\text{ADE}}}}{{{\text{Area}}{\text{ }}\Delta {\text{ABC}}}} = \dfrac{1}{9}\] so we have that \[{\text{Area of }}\Delta {\text{ADE}} = \dfrac{{{\text{Area of }}\Delta {\text{ABC}}}}{9}\]. Calculating it by substituting, \[{\text{Area of}}\Delta {\text{ABC = 7}}{\text{.5}}\]:
\[ \Rightarrow {\text{Area of }}\Delta {\text{ADE}} = \dfrac{{7.5}}{9}\]
By simplifying the RHS side:
\[{\text{Area of }}\Delta {\text{ADE}} = \dfrac{5}{6}\]
Students should remember the similarity properties very well.