Question

In the figure, the blocks A, B, and C of mass m each have acceleration ${a_1}$​, ${a_2}$​ and ${a_3}$​ respectively. \[{F_1}\]​and \[{F_2}\]are external forces of magnitude 2mg and mg respectively. Then

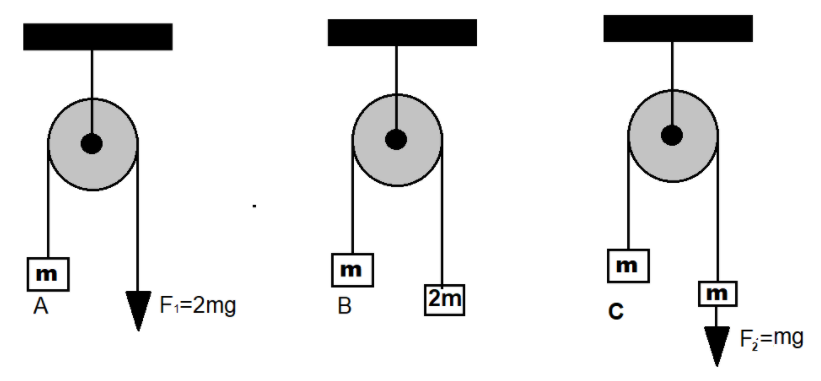
A. ${a_1} = {a_2} = {a_3}$
B. ${a_1} > {a_3} > {a_2}$
C. ${a_1} = {a_2},{a_2} > {a_3}$
D. \[{a_1} > {a_2},{a_2} = {a_3}\]

Answer 1

Hint: Whenever a mass is suspended from a point by a thread or anything there is a force of tension that acts in the thread which is equal to the weight of the body and in an upwards direction. A body is set in motion only when it is under the action of a residuary unbalanced force. The motion of the body will always be in the direction of the unbalanced residuary force.

Complete step by step answer:
To solve such kind of problems we draw a free body diagram of each option and try to find out the value of acceleration in each case

Figure 1:

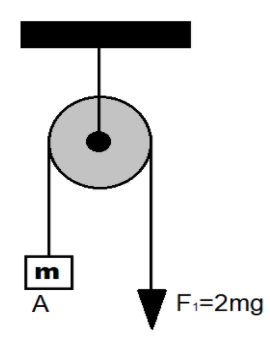
Its free body diagram (we are only considering the pulley and mass system the upper joint of pulley is neglected as it will be the same in each case )

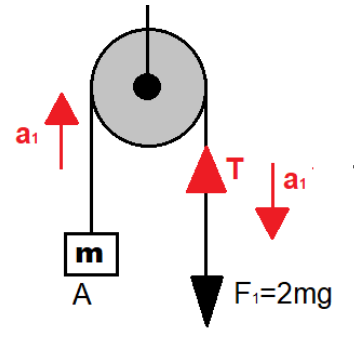
Now equating the equations we get
$F = T$
$T - mg = m{a_1}$
$\because {F_1} = 2mg$
$\therefore m{a_1} = 2mg - mg$
$ \Rightarrow m{a_1} = mg$
$ \Rightarrow {a_1} = g \downarrow $ -----(1)

Figure 2:

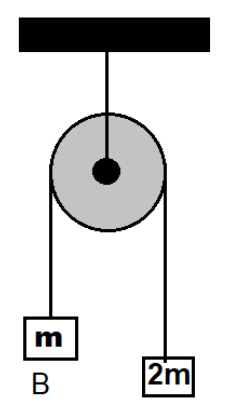
Its free body diagram

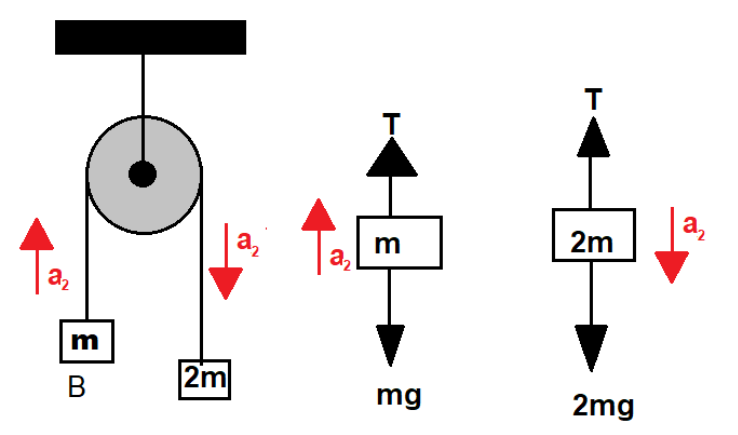
Writing mass equations for balanced forces
$T - mg = m{a_2}$
$2mg - T = 2m{a_2}$
Solving the above two equation for ${a_2}$ we get
$T - mg + 2mg - T = m{a_2} + 2m{a_2}$
$ \Rightarrow mg = 3m{a_2}$
$ \Rightarrow {a_2} = \dfrac{g}{3}$ ----(2)

Figure 3 :

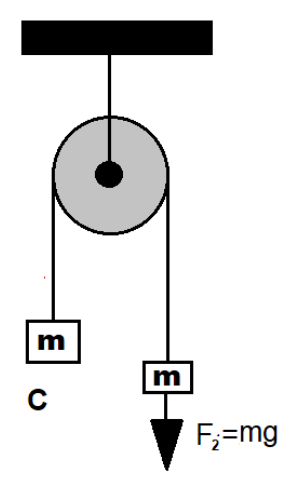
Its free body diagram

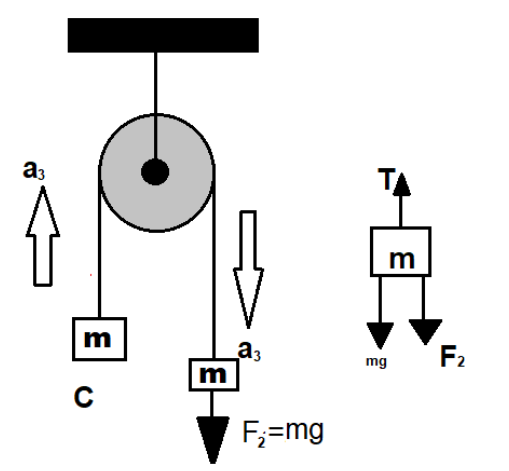
Writing the mass equation or force balance equation
${F_2} + mg - T = m{a_3}$
$\because {F_2} = mg$
$\therefore 2mg - T = m{a_3}$
And for the left box $T - mg = m{a_3}$
Solving the above two equations we get
\[2mg - T + T - mg = 2m{a_3}\]
\[ \Rightarrow mg = 2m{a_3}\]
\[ \Rightarrow {a_3} = \dfrac{g}{2}\]
Now we have got accelerations for all the three cases
${a_1} = g$, ${a_2} = \dfrac{g}{3}$ , \[{a_3} = \dfrac{g}{2}\]
Now as we can see: ${a_1} > {a_3} > {a_2}$

Hence, the correct answer is option (B).

Note: The mass will move in the direction same as that of the resulting unbalanced force. In general, in cases when mass is simply suspended the tension will always work opposite to gravity. If a suspended mass system is at rest this means all the acting forces have been balanced by each other in such a way that there is no unbalanced force to set the mass in motion.