Question

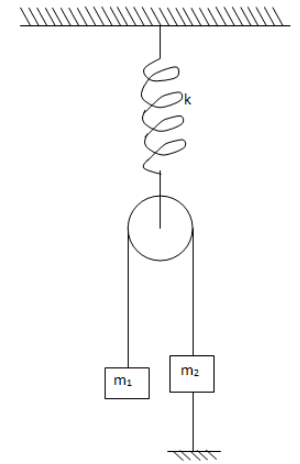
In the figure shows, pulley and spring are ideal. Find the potential energy stored in the spring (\[{m_1} > {m_2}\])

Answer 1

Hint:We are asked to find the potential energy stored in the spring. First, recall the formula to find potential energy stored in a spring. Draw a free body diagram of the problem. Using this diagram, find the value of displacement and use this value to find potential energy of the spring.

Complete step by step answer:
Given a figure where pulley and spring are ideal.The formula to find potential energy stored in a spring is,
\[P.E = \dfrac{1}{2}k{x^2}\] (i)
where \[k\] is the spring constant and \[x\] is the displacement from the mean position.
Let us draw the free body diagram for the problem.

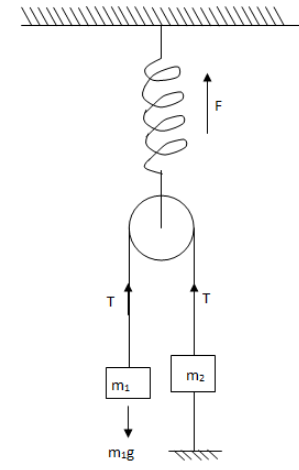
In the figure, \[F\] is the restoring force of the spring, \[T\] is the tension on the string and \[g\] is acceleration due to gravity.
Restoring force is given by the formula,
\[F = kx\] (ii)
where \[k\] is the spring constant and \[x\] is the displacement from the mean position.
From the figure we observe,
\[T + T = F\]
Putting the value of \[F\] we get,
\[T + T = kx\]
\[ \Rightarrow 2T = kx\]
\[ \Rightarrow T = \dfrac{1}{2}kx\] (iii)
From the figure we get,
\[T = {m_1}g\]
Putting the value of \[T\] we get,
\[\dfrac{1}{2}kx = {m_1}g\]
\[ \Rightarrow x = \dfrac{{2{m_1}g}}{k}\]
Now, putting this value of \[x\] in equation (i) we get the potential energy as,
\[P.E = \dfrac{1}{2}k{\left( {\dfrac{{2{m_1}g}}{k}} \right)^2}\]
\[ \Rightarrow P.E = \dfrac{1}{2}k\left( {\dfrac{{4{m_1}^2{g^2}}}{{{k^2}}}} \right)\]
\[ \therefore P.E = \dfrac{{2{m_1}^2{g^2}}}{k}\]

Therefore the potential energy stored in the spring is \[\dfrac{{2{m_1}^2{g^2}}}{k}\].

Note:For such types of problems, before proceeding for calculations, draw a free body diagram. A free body diagram is a diagram showing the forces and their directions acting on a given system. Here we have used the term restoring force, restoring force is the force which brings back an object to its mean position or equilibrium.