Question

In the figure shown, square 2 is formed by joining the mid-points of square 1, square 3 is formed by joining the mid-points of square 2 and so on. In this way a total five squares are drawn. The side of square 1 is ‘a’ cm. What is the sum of perimeters of all the five squares?

Answer 1

Hint:Here in this question we are seeing that square 2 formed by joining the mid-points of square 1. So Square 2 is dividing the sides of square 1 into two equal halves and forming four right angled triangles at every corner of Square 1.

Complete step-by-step answer:

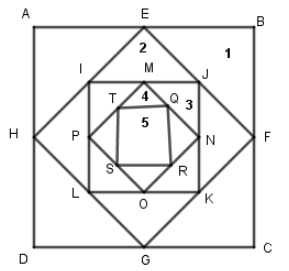
Sides of square 1 = ‘a’ cm
Perimeter of square 1 = 4 × a = 4a cm.
AB = BC = CD = DA = ‘a’ cm
Square 2 bisects every side of square 1 and form a right angled triangle.
In $\vartriangle EBF$
              EB = BF = a2 and $\angle B = {90^ \circ }$
 Now we will use Pythagoras theorem in which we know that in a right angled triangle the square of the side opposite to the right angle is equal to the sum of squares of the other two sides.
Thus,
$
  E{F^2} = E{B^2} + B{F^2} \\
   \Rightarrow E{F^2} = {\left( {\dfrac{a}{2}} \right)^2} + {\left( {\dfrac{a}{2}} \right)^2} \\
   \Rightarrow E{F^2} = \dfrac{{{a^2}}}{4} + \dfrac{{{a^2}}}{4} \\
  \therefore E{F^2} = \dfrac{{{a^2}}}{2} \Rightarrow EF = \dfrac{a}{{\sqrt 2 }} \\
 $
Sides of Square 2 = $\dfrac{a}{{\sqrt 2 }}$
Perimeter of Square 2 = $4 \times \dfrac{a}{{\sqrt 2 }}$= $2\sqrt 2 a$cm (Perimeter of Square is sum of all the four sides)
Now we will find the length of the side of square 3
In $\vartriangle MJN$
MJ = JN = $\dfrac{1}{2} \times \dfrac{a}{{\sqrt 2 }} = \dfrac{a}{{2\sqrt 2 }}$ cm (Square 3 bisects the sides of square 2 and form right angle triangle).
Now we will use Pythagoras theorem in which we know that in a right angled triangle the square of the side opposite to the right angle is equal to the sum of squares of the other two sides.
Thus,
$
  I{J^2} = E{J^2} + E{I^2} \\
   \Rightarrow I{J^2} = {\left( {\dfrac{a}{{2\sqrt 2 }}} \right)^2} + {\left( {\dfrac{a}{{2\sqrt 2 }}} \right)^2} \\
   \Rightarrow I{J^2} = \dfrac{{{a^2}}}{4} \\
  \therefore IJ = \dfrac{a}{2}cm \\
 $
Perimeter of square 3 = $4 \times \dfrac{a}{2} = 2a$cm
Now we will find the length of the sides of square 4
\[
  In\vartriangle MJN \\
  MJ = JN = \dfrac{1}{2} \times IJ = \dfrac{1}{2} \times \dfrac{a}{2} = \dfrac{a}{4}cm \\
  \angle J = {90^ \circ } \\
 \]
Now we will use Pythagoras theorem in which we know that in a right angled triangle the square of the side opposite to the right angle is equal to the sum of squares of the other two sides.
Thus,
$
  M{N^2} = M{J^2} + J{N^2} \\
   \Rightarrow M{N^2} = {\left( {\dfrac{a}{4}} \right)^2} + {\left( {\dfrac{a}{4}} \right)^2} \\
   \Rightarrow M{N^2} = \dfrac{{{a^2}}}{8} \\
  \therefore MN = \dfrac{a}{{2\sqrt 2 }}cm \\
 $
Perimeter of Square 4 = $4 \times \dfrac{a}{{2\sqrt 2 }} = \sqrt 2 a$cm.
Similarly we will find the length of the sides of square 5.
 $
  \vartriangle RNS \\
  RN = SN = \dfrac{1}{2}MN = \dfrac{1}{2} \times \dfrac{a}{{2\sqrt 2 }} = \dfrac{a}{{4\sqrt 2 }} \\
  \angle N = {90^ \circ } \\
 $ (KO bisects KL)
Now we will use Pythagoras theorem in which we know that in a right angled triangle the square of the side opposite to the right angle is equal to the sum of squares of the other two sides.
Thus,
$
  R{S^2} = R{N^2} + S{N^2} \\
   \Rightarrow R{S^2} = {\left( {\dfrac{a}{{4\sqrt 2 }}} \right)^2} + {\left( {\dfrac{a}{{4\sqrt 2 }}} \right)^2} \\
   \Rightarrow R{S^2} = \dfrac{{{a^2}}}{{16}} \\
  \therefore RS = \dfrac{a}{4}cm \\
 $
Perimeter of square 5 = $4 \times \dfrac{a}{4} = a$cm
Perimeter of all the five squares = $4a + 2\sqrt 2 a + 2a + \sqrt 2 a + a = 7a + 3\sqrt 2 a$cm (Ans.)

Note:
In this question we will try to find the length of the sides of square 2, square 3, square 4 and square 5 by using Pythagoras formula because square 1 and square 2 form four right angled triangle at the corner, Similarly square 3 form four right angled triangle at the corner of square 2 . By using Pythagoras formula we will find hypotenuse which would be the length of the side of Inner Square.