Question

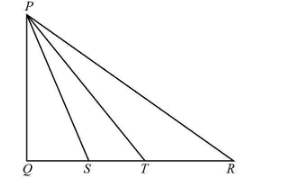
In the figure, S and T trisect the side QR of a right triangle PQR
Prove that ${\rm{8 P}}{{\rm{T}}^2} = 3{\rm{P}}{{\rm{R}}^2} + 5{\rm{P}}{{\rm{S}}^2}$

Answer 1

Hint: This question is based on Trigonometry. In this question, a right-angled triangle is given and also two points in the base of the triangle trisect the base of the triangle into three equal parts. By doing so, there are now three right-angled triangles and in order to find the relation between them, we use the Pythagoras Theorem.

Complete step-by-step answer:
In the given right-angled triangle $\Delta PQR$ two points S and T trisect the side QR into three equal parts. Which means that,
\[
QS{\rm{ }} = {\rm{ }}ST{\rm{ }}\\
 = {\rm{ TR}}
\]
Let us assume the value of \[QS{\rm{ }} = {\rm{ }}ST{\rm{ }} = {\rm{ TR}}\] is $x$ then,
\[
\;QS{\rm{ }} = {\rm{ }}ST{\rm{ }}\\
 = {\rm{ }}TR\\
{\rm{ }} = {\rm{ }}x
\]
From the $\Delta PQR$ we have,
\[
QR{\rm{ }} = {\rm{ }}QS + ST + TR\\
 = x + x + x\\
 = 3x
\]
And,
\[
QT{\rm{ }} = {\rm{ }}QS + ST\\
 = x + x\\
 = 2x
\]
Now applying the Pythagoras Theorem in the right-angled triangle $\Delta PQR$ we get,
\[P{R^{2\;}} = {\rm{ }}P{Q^2}\; + {\rm{ }}Q{R^2}\]
Substituting the value of $QR$ in the expression we get,
\[
{P{R^{2\;}} = {\rm{ }}P{Q^2}\; + {{\left( {3x} \right)}^2}}\\
{P{R^{2\;}} = {\rm{ }}P{Q^2}\; + {\rm{ }}9{x^2}}
\]
Similarly, applying Pythagoras Theorem in the right-angled triangle $\Delta PQT$ we get,
\[P{T^2}\; = {\rm{ }}P{Q^{2\;}} + {\rm{ Q}}{T^2}\]
Substituting the value of $QT$ in the expression we get,
\[
{P{T^2}\; = {\rm{ }}P{Q^{2\;}} + {\rm{ }}{{\left( {2x} \right)}^2}}\\
{P{T^2}\; = {\rm{ }}P{Q^{2\;}} + {\rm{ }}4{x^2}}
\]
And, applying Pythagoras Theorem in the right-angled triangle$\Delta PQS$ we get,
\[P{S^2}\; = {\rm{ }}P{Q^2}\; + Q{S^2}\]
Substituting the value of $QS$ in the expression we get,
\[P{S^2}\; = {\rm{ }}P{Q^2}\; + {x^2}\]
We have to prove that,
${\rm{8 P}}{{\rm{T}}^2} = 3{\rm{P}}{{\rm{R}}^2} + 5{\rm{P}}{{\rm{S}}^2}$
Substituting the values of $PT,PR{\rm{ and }}PS$ that we have calculated in this expression, we get,
\[
8\left( {P{Q^{2\;}} + {\rm{ }}4{x^2}} \right){\rm{ }} = 3\left( {P{Q^2}\; + {\rm{ }}9{x^2}} \right){\rm{ + }}5{\rm{ }}\left( {P{Q^2}\; + {\rm{ }}{x^2}} \right)\\
8P{Q^{2\;}} + {\rm{ }}32{x^2} = 3P{Q^2}\; + {\rm{ }}27{x^2}\; + {\rm{ }}5P{Q^2}\; + {\rm{ }}5{x^2}\\
8P{Q^{2\;}} + {\rm{ }}32{x^2} = \;8P{Q^{2\;}} + {\rm{ }}32{x^2}
\]
Therefore, LHS = RHS.
Hence, it is proven that ${\rm{8 P}}{{\rm{T}}^2} = 3{\rm{P}}{{\rm{R}}^2} + 5{\rm{P}}{{\rm{S}}^2}$

Note: The alternate method of solving this question was to take either LHS or RHS of the expression that we have to prove and get the other side of the expression from it.
For example, taking the RHS of the expression we have,
$
3{\rm{P}}{{\rm{R}}^2} + 5{\rm{P}}{{\rm{S}}^2} = 3\left( {P{Q^2}\; + {\rm{ }}9{x^2}} \right){\rm{ + }}5{\rm{ }}\left( {P{Q^2}\; + {\rm{ }}{x^2}} \right)\\
 = 3P{Q^2}\; + {\rm{ }}27{x^2}\; + {\rm{ }}5P{Q^2}\; + {\rm{ }}5{x^2}\\
 = 8P{Q^{2\;}} + {\rm{ }}32{x^2}
$
We know that \[P{T^2}\; = {\rm{ }}P{Q^{2\;}} + {\rm{ }}4{x^2}\] or \[\;{\rm{ }}P{Q^{2\;}} = P{T^2}{\rm{ - }}4{x^2}\]
Substituting this value in the expression we get,
$
3{\rm{P}}{{\rm{R}}^2} + 5{\rm{P}}{{\rm{S}}^2} = 8\left( {P{T^2}{\rm{ - }}4{x^2}} \right) + {\rm{ }}32{x^2}\\
 = 8P{T^2} - 32{x^2} + 32{x^2}\\
 = 8P{T^2}
$
Therefore, RHS = LHS.