Question

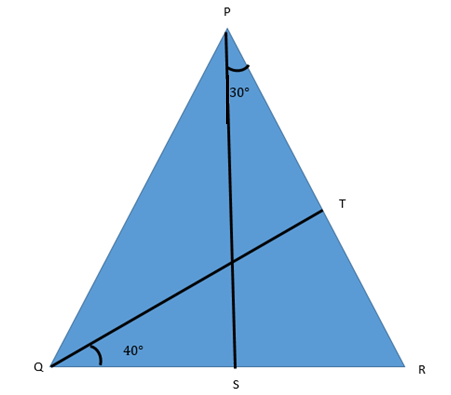
In the figure, \[QT \bot PR,\angle TQR = {40^ \circ }\] and \[\angle SPR = {30^ \circ }\]. Find \[\angle TRS\] and \[\angle PSQ\].

Answer 1

Hint: We will first of all consider the $\vartriangle TQR$ and apply the angle sum property to it to get the required \[\angle TRS\]. Now, we will consider $\vartriangle PSR$ and apply the angle sum property to it as well to obtain the value of \[\angle PSR\] and find its supplementary angle.

Complete step-by-step solution:
The students must know that the sum of all the interior angles of a triangle is always equal to ${180^ \circ }$.
Consider the $\vartriangle TQR$ in this figure. It also must follow the angle sum property.
$ \Rightarrow \angle TQR + \angle QRT + \angle RTQ = {180^ \circ }$
Now, since we are already given that \[QT \bot PR\] and \[\angle TQR = {40^ \circ }\]. Therefore, we can rewrite the above expression as follows:-
$ \Rightarrow {40^ \circ } + \angle QRT + {90^ \circ } = {180^ \circ }$
Taking the angles value from addition in LHS to subtraction in RHS to get:-
$ \Rightarrow \angle QRT = {180^ \circ } - {130^ \circ }$
Simplifying the calculation in RHS in the above expression to get:-
$ \Rightarrow \angle QRT = {50^ \circ }$
\[\therefore \angle TRS = {50^ \circ }\] ………….(1)
Now, we will consider the $\vartriangle PSR$ in this figure. It also must follow the angle sum property.
$ \Rightarrow \angle SPR + \angle PRS + \angle RSP = {180^ \circ }$
Now, since we are already given that \[\angle PRS = {50^ \circ }\](Using 1) and \[\angle SPR = {30^ \circ }\]. Therefore, we can rewrite the above expression as follows:-
$ \Rightarrow {30^ \circ } + {50^ \circ } + \angle RSP = {180^ \circ }$
Taking the angles value from addition in LHS to subtraction in RHS to get:-
$ \Rightarrow \angle RSP = {180^ \circ } - {80^ \circ }$
Simplifying the calculation in RHS in the above expression to get:-
$ \Rightarrow \angle RSP = {100^ \circ }$ ……………….(2)
Now, since $\angle RSP$ and \[\angle PSQ\] are linear. Therefore, we will have:-
$ \Rightarrow \;\angle RSP + \angle PSQ = {180^ \circ }$
Putting in the equation (2) to get as follows:-
$ \Rightarrow \;\angle PSQ = {80^ \circ }$

$\therefore $ We have: \[\angle TRS = {50^ \circ }\] and $\angle PSQ = {80^ \circ }$.

Note: The students must note that the angles on a straight line is known as a straight angle which is always equal to ${180^ \circ }$. It may be divided into any number of angles. Those will together form ${180^ \circ }$ only. Like here, we had $\angle RSP$ and \[\angle PSQ\] forming the straight angle on a line together. Therefore, these both angles are known as supplementary angles or linear angles as well.
The students must note that the property we used in the question which states that the sum of all the interior angles of a triangle is always equal to ${180^ \circ }$. This property of triangles is known as the “Angle sum property” of triangles.