Question

In the figure, pulley is light and smooth. Thread is massless. On applying force F, KE increases by 20 J in 1 s.

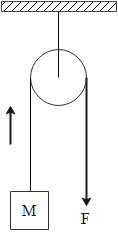
A. tension in the string is Mg
B. the tension in the string is F
C. work done by the tension in 1 s is 20 J.
D. the work done by the force of gravity is 20 J in 1 s.

Answer 1

Hint: Tension is produced in a string when a force is applied on it. We can calculate the work done by tension in the string and the force of gravity is making use of the work-energy theorem which states that work done by a system is equal to the change in its kinetic energy.

Formula used:
The work energy theorem for a mechanical system is given as
$\dfrac{1}{2}m\left( {{v^2} - {u^2}} \right) = W$

Complete answer:
We are given a pulley system where a mass m is suspended from one side while a force F is applied from the other side. As a result of the force applied on the other side of the pulley, a tension is produced in the string which helps in pulling up the load from the other end. Therefore, the tension in the string is equal to the force F applied on the other end of the string.
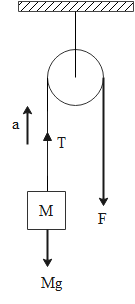
Next, let us draw the free body diagram showing the direction of the tension acting on the string.
We can see in the diagram that there is tension T and acceleration acting in upward direction and force due to weight of block acting in downward direction. Based on this we can write the following expression.
$T - Mg = Ma$ …(i)

Next, let us apply the work energy theorem on the motion of the pulley. Let the initial velocity of the block be zero. We are given that on applying force F, KE increases by 20 J in 1 s. This means total work done by the system is 20 J in 1 s.
Then we can write
$
  \dfrac{1}{2}M\left( {{v^2} - 0} \right) = 20 \\
   \Rightarrow v = \sqrt {\dfrac{{40}}{M}} \\
 $
Here in the first line, the left side represents the change in kinetic energy of the system while the right hand side is the work done.

As we know that $v = u + at$, inserting known values, we get

$
  \sqrt {\dfrac{{40}}{M}} = 0 + a\left( 1 \right) \\
   \Rightarrow a = \sqrt {\dfrac{{40}}{M}} \\
  T - Mg = M \times \sqrt {\dfrac{{40}}{M}} = \sqrt {40M} \\
   \Rightarrow T > Mg \\
 $

Now the sum of work done by tension and gravity is 20 J.
${W_T} + {W_{Mg}} = 20J$
Work done by Mg is negative because the object is going upwards. This implies that in order to keep the above expression true, the work done by tension must be positive and greater than 20J.

So, the correct answer is “Option B”.

Note:
1. The prime advantage of pulley is that by using this system, we can change the direction in which the force needs to be applied in order to lift a load from the other end of the string.
2. In gravity, if an object moves upwards then work done is negative while if it moves downwards then work done is positive.