Question

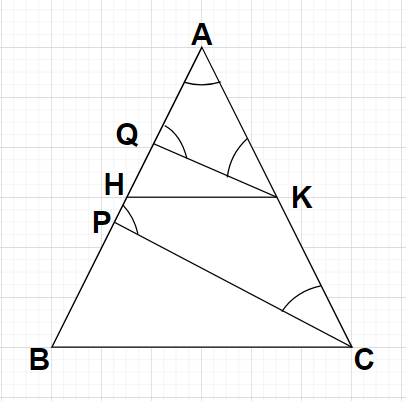
In the figure, PC $\parallel $QK and BC$\parallel $ HK. If AQ=6 cm, QH=4 cm, HP=5 cm, KC=18 cm, then find AK.

Answer 1

Hint: Here, we will be proceeding by observing the two triangles i.e., $\vartriangle $AQK and $\vartriangle $APC. By AAA congruence rule we will prove that both of these triangles are congruent and then we will use the property of congruent triangles i.e., if any two triangles are congruent then the ratio of their corresponding sides will be equal.

Complete step-by-step answer:
Given, PC $\parallel $QK and BC $\parallel $HK
Also it is given that AQ=6 cm, QH=4 cm, HP=5 cm and KC=18 cm
Since, the side PC is parallel to the side QK in the triangle shown. So, the corresponding angles will be equal.
i.e., $\angle {\text{AQK}} = \angle {\text{APC}}$ and $\angle {\text{AKQ}} = \angle {\text{ACP}}$ because these are the sets of corresponding angles.
In $\vartriangle $AQK and $\vartriangle $ APC, we have
$\angle {\text{A}} = \angle {\text{A}}$ [Common angle in both the considered triangles]
$\angle {\text{AQK}} = \angle {\text{APC}}$
$\angle {\text{AKQ}} = \angle {\text{ACP}}$
Therefore, the two considered triangles i.e., $\vartriangle $AQK and $\vartriangle $ APC are congruent to each other by AAA (Angle-Angle-Angle) congruence rule.
i.e., \[\vartriangle {\text{AQK}} \cong \vartriangle {\text{APC}}\]
Also, we know that if any two triangles are congruent then the ratio of their corresponding sides will be equal.
Since, \[\vartriangle {\text{AQK}} \cong \vartriangle {\text{APC}}\]
So, we can write $\dfrac{{{\text{AQ}}}}{{{\text{AP}}}} = \dfrac{{{\text{AK}}}}{{{\text{AC}}}}{\text{ }} \to {\text{(1)}}$
Since, we know that the side AP is the sum of AQ, QH and HP i.e., AP=AQ+QH+HP and the side AC is the sum of AK and KC i.e., AC=AK+KC
By substituting these value of sides AP and AC in equation (1), we get
$ \Rightarrow \dfrac{{{\text{AQ}}}}{{{\text{AQ}} + {\text{QH}} + {\text{HP}}}} = \dfrac{{{\text{AK}}}}{{{\text{AK}} + {\text{KC}}}}$
By substituting AQ=6 cm, QH=4 cm, HP=5 cm and KC=18 cm in the above equation, we get
$
   \Rightarrow \dfrac{{\text{6}}}{{{\text{6}} + 4 + {\text{5}}}} = \dfrac{{{\text{AK}}}}{{{\text{AK}} + 18}} \\
   \Rightarrow \dfrac{{\text{6}}}{{15}} = \dfrac{{{\text{AK}}}}{{{\text{AK}} + 18}} \\
 $
By cross multiplication of the above equation, we get
$
   \Rightarrow {\text{6}}\left( {{\text{AK}} + 18} \right) = {\text{15AK}} \\
   \Rightarrow {\text{6AK}} + 108 = {\text{15AK}} \\
   \Rightarrow {\text{15AK}} - {\text{6AK = 108}} \\
   \Rightarrow 9{\text{AK = 108}} \\
   \Rightarrow {\text{AK = }}\dfrac{{{\text{108}}}}{9} = 12{\text{ cm}} \\
 $
Therefore, the length of AK is 12 cm.

Note: In this particular problem, we have considered triangles $\vartriangle $AQK and $\vartriangle $APC because of the input data given (i.e., AQ=6 cm, QH=4 cm, HP=5 cm, KC=18 cm ). Also, the pairs of the corresponding sides in triangles $\vartriangle $AQK and $\vartriangle $APC are AQ and AP, AK and AC, QK and PC. Hence, we can write that $\dfrac{{{\text{AQ}}}}{{{\text{AP}}}} = \dfrac{{{\text{AK}}}}{{{\text{AC}}}} = \dfrac{{{\text{QK}}}}{{{\text{PC}}}}$.