Question

In the figure, $PA$ and $PB$ are tangents to the circle with centre $O$ such that $\angle APB={{50}^{\circ }}$ . Write measure of $\angle OAB$ .

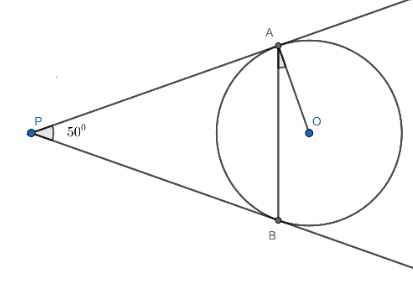
Answer 1

Hint: For solving this question first we will see that sum of interior angles of a triangle is always ${{180}^{0}}$ and angles opposite to equal sides of an isosceles triangle are equal. After that, we will see that tangent to the circle is perpendicular to the radius of the circle at the point of contact and if two tangents are drawn from an external point of the circle, then they are of equal lengths. Then, we will use them to find the correct answer to this question.

Complete step-by-step solution -
Given:
In the figure, $PA$ and $PB$ are tangents to the circle with center $O$ such that $\angle APB={{50}^{\circ }}$. And we have to find the measure of $\angle OAB$.

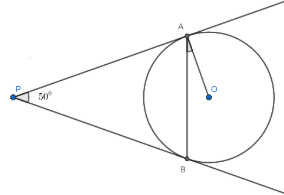
Now, before we proceed we will see 2 important properties related to triangles.
First property:
The Sum of interior angles of a triangle is always ${{180}^{0}}$. It is a very basic property but very useful and important.
Second property:
Angles opposite to equal sides of an isosceles triangle are equal. This can be understood with the help of the figure below:

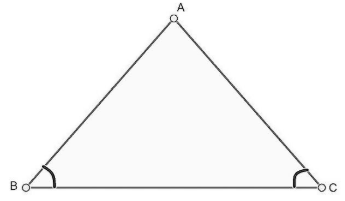
In the above figure, $\Delta ABC$ is shown in which $AB=AC$. Then, $\angle ABC=\angle ACB$.
Now, before we proceed, we should know the following two important theorems of the circle:
Theorem 1:
Statement: The tangent to the circle is perpendicular to the radius of the circle at the point of contact. For more clarity, look at the figure given below:

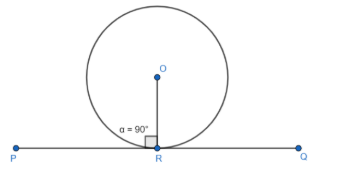
In the above figure, PQ is a tangent at point R on the circle and $\angle ORP=\angle ORQ={{90}^{\circ }}$.
Theorem 2:
Statement: If two tangents are drawn from an external point of the circle, then they are of equal lengths. For more clarity, look at the figure given below:

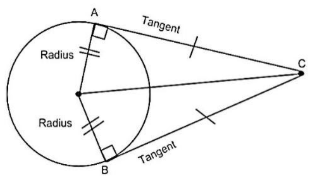
In the above figure, AC and BC are tangent from an external point C and $AC=BC$.
Now, we will be using the above theorems to solve this question.
As we have the following figure:

Now, in the above figure, PA, PB are tangent from an external point P and as we know that, if two tangents are drawn from an external point of the circle, then they are of equal lengths. Then,
$PA=PB$
Now, from the above result we conclude that in $\Delta PAB$ , length of side PA is equal to PB so, $\Delta PAB$ will be an isosceles triangle and as we know that, angles opposite to equal sides of an isosceles triangle are equal. Then,
$\angle PBA=\angle PAB........\left( 1 \right)$
Now, as we know that, the sum of interior angles of a triangle is always ${{180}^{0}}$ so, we will use this result for $\Delta PAB$ . Then,
$\angle APB+\angle PAB+\angle PBA={{180}^{\circ }}$
Now, as it is given that $\angle APB={{50}^{\circ }}$ and we can put $\angle PBA=\angle PAB$ from equation (1) in the above equation. Then,
$\begin{align}
  & \angle APB+\angle PAB+\angle PBA={{180}^{\circ }} \\
 & \Rightarrow {{50}^{\circ }}+\angle PAB+\angle PAB={{180}^{\circ }} \\
 & \Rightarrow 2\angle PAB={{180}^{\circ }}-{{50}^{\circ }} \\
 & \Rightarrow 2\angle PAB={{130}^{\circ }} \\
 & \Rightarrow \angle PAB={{65}^{\circ }}..................................\left( 2 \right) \\
\end{align}$
Now, as we know that, tangent to the circle is perpendicular to the radius of the circle at the point of contact so, measure of $\angle OAP={{90}^{\circ }}$ and we can write $\angle OAP=\angle OAB+\angle PAB$ . Then,
$\begin{align}
  & \angle OAP={{90}^{\circ }} \\
 & \Rightarrow \angle OAB+\angle PAB={{90}^{\circ }} \\
\end{align}$
Now, we will substitute $\angle PAB={{65}^{\circ }}$ from equation (2) in the above equation. Then,
$\begin{align}
  & \angle OAB+\angle PAB={{90}^{\circ }} \\
 & \Rightarrow \angle OAB+{{65}^{\circ }}={{90}^{\circ }} \\
 & \Rightarrow \angle OAB={{90}^{\circ }}-{{65}^{\circ }} \\
 & \Rightarrow \angle OAB={{25}^{\circ }} \\
\end{align}$
Now, from the above result, we conclude that the measure of the $\angle OAB={{25}^{\circ }}$.

Note: Here, the student should first understand what is asked in the question and then proceed in the right direction to get the correct answer quickly. Moreover, though the question is very easy, but we should apply the theorems and results related to the circles and triangles with full clarity so, that we can find the correct answer easily.