Question

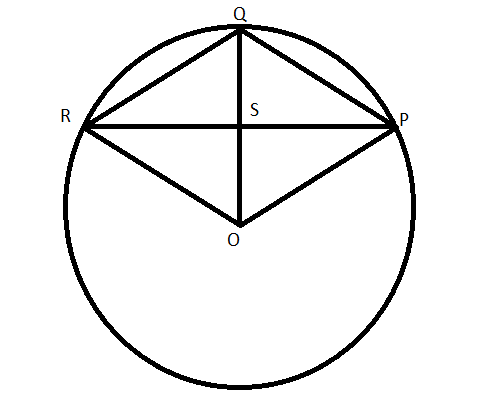
In the figure, OPQR is a rhombus, 3 of whose vertices lie on the circle with centre O. If the area of the rhombus is $32\sqrt{3}c{{m}^{2}}$, find the radius of the circle.

Answer 1

Hint: As given in the question, OPQR is a rhombus, then RO = OP = OR = PQ because the sides of rhombus are equal. Now, consider two equilateral triangles $\Delta RQO\text{ and }\Delta QOP$ and add their areas after converting the areas in the form of radius as one side of rhombus are equal to radius of circle. By using this we can easily find the value of ‘R’ which is our radius.

Complete step-by-step answer:

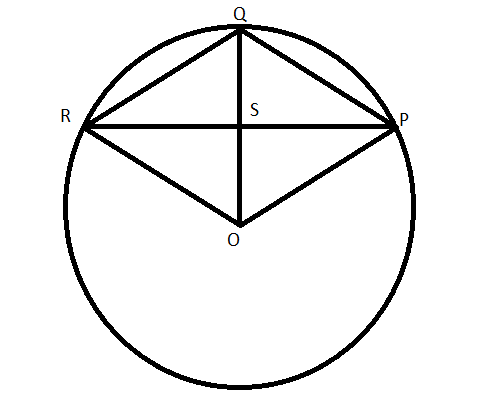
In the circle given in the figure, we let the length of the radius of the circle be ‘R’. Inside the circle, one rhombus is given. In rhombus OPQR, the length of all sides are equal and the length of both diagonals are also equal.
$RO=OP=QR=PQ$(side of Rhombus)
$OQ=R$(Radius of the circle)
Now, we are taking two triangles $\Delta RQO\text{ and }\Delta QOP$.
They are equilateral triangles because RO = QR (sides of rhombus) and OQ is the radius. Since, RO is also depicting radius as shown in figure so RO = OQ. Hence, all sides are equal.
Now, the area of rhombus is given by:
Area of Rhombus = Area of equilateral triangle RQO + Area of equilateral triangle QOP.
As we know that for an equilateral triangle, the area is $\dfrac{\sqrt{3}}{4}{{a}^{2}}$, where a is the dimension of the equilateral side.
$\begin{align}
  & \therefore \dfrac{\sqrt{3}}{4}{{R}^{2}}+\dfrac{\sqrt{3}}{4}{{R}^{2}}=32\sqrt{3} \\
 & \dfrac{\sqrt{3}}{2}{{R}^{2}}=32\sqrt{3} \\
 & \Rightarrow R=\pm 8cm \\
\end{align}$
Since, the dimension of a fixed quantity can never be negative so neglecting the negative value of radius.
Hence, the dimension of radius ‘R’ is 8cm.

Note: The key step in solving this problem is the knowledge of geometrical figures particularly rhombus and circle. By using some properties and visual observation we can easily identify the measurement of radius of circle with conclusive evidence. These observation skills will enhance the confidence of students.