Question

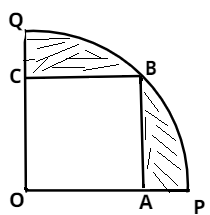
In the figure , \[OABC\]is a square inscribed in a quadrant \[OPBQ\] . If \[OA = 20cm\] find the area of the shaded region. $\pi$=3.14

Answer 1

Hint:- In this question first we will find the diagonal of the square which is the radius of the quadrant, then subtract the area of the square from the area of the quadrant to get the area of the shaded region.


Complete step-by-step solution -

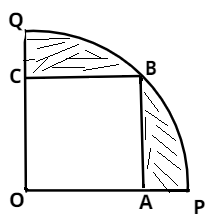
In the given figure ,
\[OABC\] is a square .
\[OA = AB = {\text{ }}20{\text{ }}cm\]
In \[\Delta OAB\]
By applying Pythagoras theorem
\[
  OB = \sqrt {{{(AB)}^2} + {{(OA)}^2}} \\
  OA = AB = 20cm\,({\text{sides of square}}) \\
\]
So,
\[OB = 20\sqrt 2 \]
Hence the radius of the quadrant is \[\;20\sqrt 2 \,cm\].

Now,
Area of shaded region = area of quadrant – area of square
Area = \[\dfrac{{\pi {r^2}}}{4} - {(AB)^2}\]
Area = \[\dfrac{{\pi {{(20\sqrt 2 )}^2}}}{4} - {20^2} = 208c{m^2}\]
Hence the area of the shaded region is \[{\text{208}}c{m^2}\].

Note – In these types of questions we have to calculate the area of the whole region then calculate the area of the divide part then calculate the small area with big area . Making diagrams will be very helpful in these types of questions.