
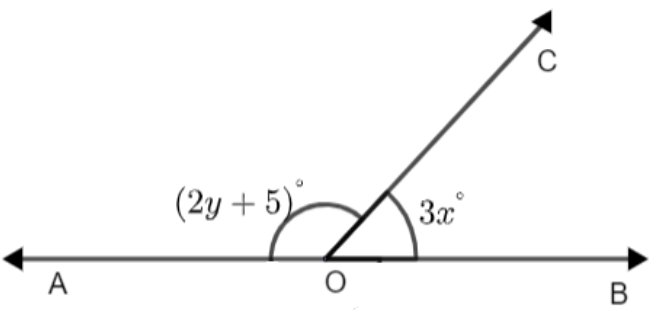
In the figure, OA and OB are opposite rays if \[x={{25}^{\circ }}\], what is the value of y?

Answer
557.1k+ views
Hint: Take the sum of the given two angles and equate it with 180 degrees by considering AOB as a straight line and the given angles as a linear pair. Substitute the value of x and solve for the value of y to get the answer.
Complete step-by-step solution
Here, we have been provided with a figure and we have been asked to find the value of y.
Clearly, we can see that AOB is a straight line and a ray is originated from O such that it forms two angles on the line AOB. One angle is given as \[3{{x}^{\circ }}\] and the other as \[{{\left( 2y+5 \right)}^{\circ }}\]. So, these angles are forming a linear pair. Let us see what is meant by a linear pair.
Now, a linear pair of angles are the angles formed when two lines intersect each other. These angles must be adjacent to each other when the lines intersect. Linear pair of angles always makes a sum of \[{{180}^{\circ }}\], i. e. they are supplementary.
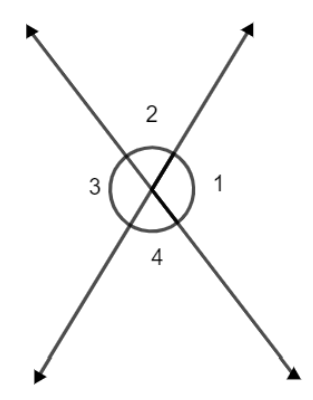
For example: - in the above figure we have assumed two lines intersecting each other at a point. Here, the pairs: - \[\left( \angle 1,\angle 2 \right);\left( \angle 2,\angle 3 \right);\left( \angle 3,\angle 4 \right)\] and \[\left( \angle 4,\angle 1 \right)\] are the four pairs of linear pair angles. So, we can write: -
\[\Rightarrow \angle 1+\angle 2=\angle 2+\angle 3=\angle 3+\angle 4=\angle 4+\angle 1={{180}^{\circ }}\]
Now, let us come to the question. So, from the figure given in the question we can write,
\[\begin{align}
& \Rightarrow 3{{x}^{\circ }}+2{{y}^{\circ }}+{{5}^{\circ }}={{180}^{\circ }} \\
& \Rightarrow 3{{x}^{\circ }}+2{{y}^{\circ }}={{175}^{\circ }} \\
\end{align}\]
Substituting \[x={{25}^{\circ }}\] in the above relation, given in the question, we get,
\[\begin{align}
& \Rightarrow 2{{y}^{\circ }}+3\times {{25}^{\circ }}={{175}^{\circ }} \\
& \Rightarrow 2{{y}^{\circ }}={{175}^{\circ }}-{{75}^{\circ }} \\
& \Rightarrow 2{{y}^{\circ }}={{100}^{\circ }} \\
& \Rightarrow {{y}^{\circ }}={{50}^{\circ }} \\
\end{align}\]
Hence the value of y is \[{{50}^{\circ }}\].
Note: One may note that here we must not use a protractor to measure the angles drawn in the figure of the question. It may be possible that we will get the wrong answer. So, we must solve it algebraically to find the value of y. Remember the several properties of linear pair angles otherwise, you will not be able to solve the question. At last, remember that the value of y is an angle so do not forget to mention degrees.
Complete step-by-step solution
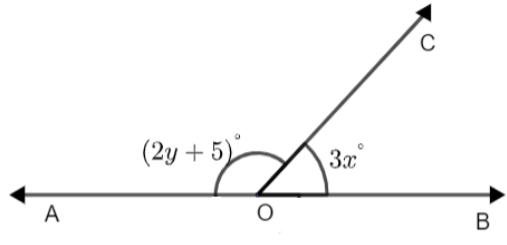
Here, we have been provided with a figure and we have been asked to find the value of y.

Clearly, we can see that AOB is a straight line and a ray is originated from O such that it forms two angles on the line AOB. One angle is given as \[3{{x}^{\circ }}\] and the other as \[{{\left( 2y+5 \right)}^{\circ }}\]. So, these angles are forming a linear pair. Let us see what is meant by a linear pair.
Now, a linear pair of angles are the angles formed when two lines intersect each other. These angles must be adjacent to each other when the lines intersect. Linear pair of angles always makes a sum of \[{{180}^{\circ }}\], i. e. they are supplementary.

For example: - in the above figure we have assumed two lines intersecting each other at a point. Here, the pairs: - \[\left( \angle 1,\angle 2 \right);\left( \angle 2,\angle 3 \right);\left( \angle 3,\angle 4 \right)\] and \[\left( \angle 4,\angle 1 \right)\] are the four pairs of linear pair angles. So, we can write: -
\[\Rightarrow \angle 1+\angle 2=\angle 2+\angle 3=\angle 3+\angle 4=\angle 4+\angle 1={{180}^{\circ }}\]
Now, let us come to the question. So, from the figure given in the question we can write,
\[\begin{align}
& \Rightarrow 3{{x}^{\circ }}+2{{y}^{\circ }}+{{5}^{\circ }}={{180}^{\circ }} \\
& \Rightarrow 3{{x}^{\circ }}+2{{y}^{\circ }}={{175}^{\circ }} \\
\end{align}\]
Substituting \[x={{25}^{\circ }}\] in the above relation, given in the question, we get,
\[\begin{align}
& \Rightarrow 2{{y}^{\circ }}+3\times {{25}^{\circ }}={{175}^{\circ }} \\
& \Rightarrow 2{{y}^{\circ }}={{175}^{\circ }}-{{75}^{\circ }} \\
& \Rightarrow 2{{y}^{\circ }}={{100}^{\circ }} \\
& \Rightarrow {{y}^{\circ }}={{50}^{\circ }} \\
\end{align}\]
Hence the value of y is \[{{50}^{\circ }}\].
Note: One may note that here we must not use a protractor to measure the angles drawn in the figure of the question. It may be possible that we will get the wrong answer. So, we must solve it algebraically to find the value of y. Remember the several properties of linear pair angles otherwise, you will not be able to solve the question. At last, remember that the value of y is an angle so do not forget to mention degrees.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the full form of pH?




