Question

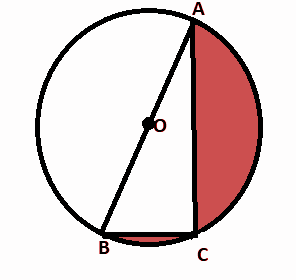
In the figure, O is the centre of a circle such that the diameter AB is equal to thirteen centimeter and AC is equal to twelve centimeter. BC is joined. Find the area of the shaded region. (Take $\pi = 3.14$ ).

Answer 1

Hint:- In this question use this concept that angle in a semicircle i.e. $\angle C = {90^\circ } $ therefore triangle ABC is a right angle triangle. So,for the right angle triangle we use the pythagorean theorem.

Complete step-by-step solution -
Given that AB is the diameter of the circle therefore angle opposite to diameter i.e. $\angle C = {90^\circ }$ according to angle in semicircle property.
Therefore triangle ABC is a right angle triangle hence applying the Pythagoras theorem we get:
$B{C^2} + A{C^2} = A{B^2}$
Given that $AB = 13$ centimeter and $AC = 12$ centimeter
Putting the values we get:
$
  B{C^2} + {12^2} = {13^2} \\
  B{C^2} = {13^2} - {12^2} \\
  B{C^2} = 169 - 144 \\
  B{C^2} = 25 \\
  BC = 5 \\
$
Area of shaded region is equal to Area of semicircle minus area of triangle ABC
As we know that area of semicircle $ = \dfrac{1}{2}\pi {r^2}$
Area of triangle $ = \dfrac{1}{2} \times {\text{base}} \times {\text{height}}$
Therefore area of shaded region $ = \dfrac{1}{2}\pi {r^2} - \dfrac{1}{2} \times {\text{base}} \times {\text{height}}$
$
   = \dfrac{1}{2} \times 3.14 \times O{A^2} - \dfrac{1}{2} \times BC \times AC \\
   = \dfrac{1}{2} \times 3.14 \times {\left( {\dfrac{{AB}}{2}} \right)^2} - \dfrac{1}{2} \times 5 \times 12 \\
   = \dfrac{1}{2} \times 3.14 \times {\left( {\dfrac{{13}}{2}} \right)^2} - 30 \\
   = \dfrac{{3.14}}{2} \times \dfrac{{169}}{4} - 30 \\
   = 36.39 \\
$
Area of the shaded region is $36.39{\text{c}}{{\text{m}}^2}$.

Note:- In this question first of all we applied the Pythagoras theorem in triangle ABC and found the value of BC which is equals to five centimeter, since area of shaded region is equal to Area of semicircle minus area of triangle ABC so we found the area of both of them using their formulas and after putting the values we got that area of shaded region is $36.39{\text{c}}{{\text{m}}^2}$.