Question

In the figure, O is the centre if $\angle BAC = x$ and $\angle BCO = y$, then

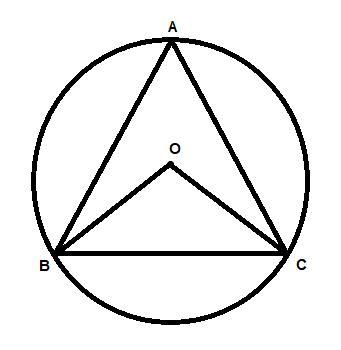
A) x + y =180
B) x + y = 90
C) x + y = 120
D) x + y = 150

Answer 1

Hint:
From the figure we have OB and OC as the radius of the circle and by the property that the angles corresponding to the equal sides are equal in a isosceles triangle we have $\angle OBC = y$ and we know that $\angle BOC = 2\angle BAC$ and considering the triangle BOC and using the angle sum property of the triangle we get the required equation.

Complete step by step solution:
We are given a figure

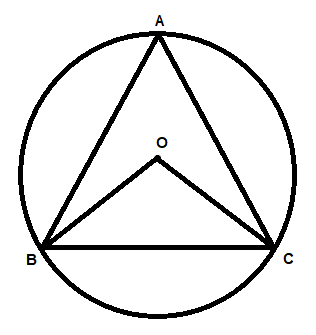
And from the figure we can see that OB = OC as OB and OC are the radius of the circle
Since the sides OB and OC of the triangle are equal then $\angle OBC = \angle OCB$
This is obtained by the property that the angles corresponding to the equal sides are equal in a isosceles triangle
Since $\angle OCB = y$ we have $\angle OBC = y$
We know that $\angle BOC = 2\angle BAC$
And we are given that $\angle BAC = x$
Therefore $\angle BOC = 2\angle BAC = 2x$
Now let's consider the triangle BOC.
And we know that the sum of the angles of a triangle is ${180^ \circ }$
Using this we get,
$
   \Rightarrow \angle OBC + \angle OCB + \angle BOC = {180^ \circ } \\
   \Rightarrow y + y + 2x = {180^ \circ } \\
   \Rightarrow 2y + 2x = {180^ \circ } \\
   \Rightarrow 2(x + y) = {180^ \circ } \\
   \Rightarrow (x + y) = \dfrac{{{{180}^ \circ }}}{2} \\
   \Rightarrow x + y = {90^ \circ } \\
$
Hence we get $x + y = {90^ \circ }$

Therefore the correct option is B.

Note:
Properties of a triangle inscribed in a triangle
1) for any triangle with one side completely on the diameter of its circumscribed circle (the circle touching all three vertices of the triangle), then this triangle must be a right triangle, with the right angle where the two shorter lines of the triangle meet the circle.
2) For any given arc, there can be any number of inscribed angles that subtend it, but only one central angle will subtend that same arc. Since the inscribed angle theorem tells us that any inscribed angle will be exactly half the measure of the central angle that subtends its arc, it follows that all inscribed angles sharing that arc will be half the measure of the same central angle. Therefore, the inscribed angles must all be congruent.