Question

In the figure (not to scale), the points M, R, N, S, Q are concyclic. Find \[\angle PQR+\angle OPR+\angle NMS+\angle OSN,\] if ‘O’ is the center of the circle.

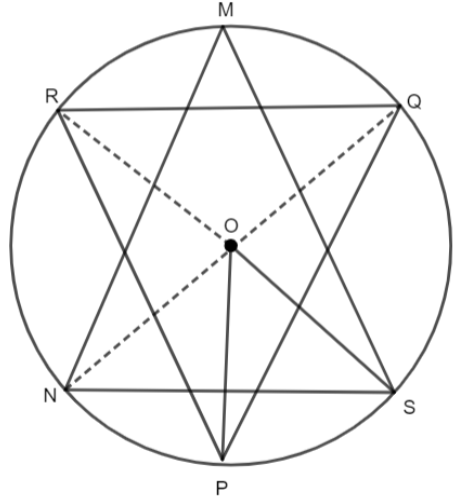
Answer 1

Hint: To solve this question we will separately consider triangle PQR and triangle MNS. In triangle PQR, we will use the theorem that ‘angle subtended by an arc on the center of the circle is twice the angle subtended by the circumference of the circle with the same arc’. After that, we will use the angle sum property of the triangle to find the sum of \[\angle OPR\] and \[\angle PQR.\] Similar process will be followed to calculate the sum of \[\angle NMS+\angle OSN.\]

Complete step-by-step solution:
Let us first consider the figure given below.

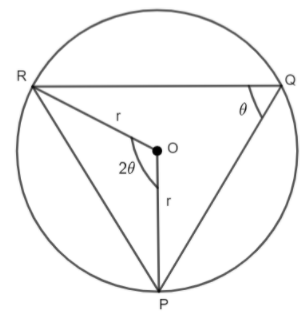
Let OR = OP = r (radius of the given circle). Now, we will apply the theorem that says “Angle subtended by an arc on the center of the circle is twice the angle subtended by the same arc on the circumference of the circle”. By applying this theorem on the minor arc RP, we have,
\[\angle ROP=2\angle RQP\]
Let
\[\angle RQP=\theta \]
\[\angle ROP=2\theta \]
Now, as OR = OP = r, we get, triangle ROP is an isosceles triangle.
Now, applying the theorem that angles opposite to equal sides are equal in triangle ROP, we have,
\[OR=OP\]
\[\angle ORP=\angle OPR\]
Let the angles be x, so we get,
\[\Rightarrow \angle ORP=\angle OPR=x\]
By the angle sum property of the triangle, we know that the sum of all the angles of a triangle is 180 degrees. Therefore, in triangle ROP, we get,
\[\angle OPR+\angle POR+\angle ORP={{180}^{\circ }}\]
\[\Rightarrow x+2\theta +x={{180}^{\circ }}\]
\[\Rightarrow 2x={{180}^{\circ }}-2\theta \]
\[\Rightarrow x=\dfrac{{{180}^{\circ }}-2\theta }{2}\]
\[\Rightarrow x={{90}^{\circ }}-\theta \]
As, \[x=\angle OPR\] and \[\theta =\angle PQR,\] so we get,
\[\angle OPR={{90}^{\circ }}-\angle PQR\]
\[\Rightarrow \angle OPR+\angle PQR={{90}^{\circ }}.......\left( i \right)\]
Now, we will consider the other part of the figure.

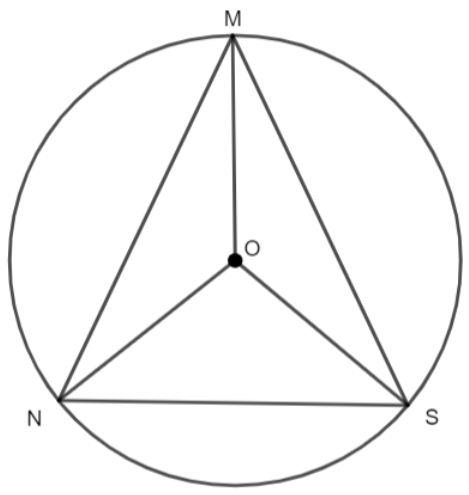
Applying the same logic as explained above in the triangle NMS given above, we have,
\[\angle NMS+\angle OSN={{90}^{\circ }}.......\left( ii \right)\]
So, adding equation (i) and (ii), we get,
\[\angle OPR+\angle PQR+\angle NMS+\angle OSN={{90}^{\circ }}+{{90}^{\circ }}\]
\[\Rightarrow \angle OPR+\angle PQR+\angle NMS+\angle OSN={{180}^{\circ }}\]
Therefore, \[{{180}^{\circ }}\] is our answer.

Note: A key point to note in this question is that while considering triangle PQR, you can consider any triangle inside of the circle to find the sum of angles PQR and OPR. But try to make sure that the triangle covered has angle PQR outside it so as to apply the theorem. Similar is the case of triangle MNS.