Question

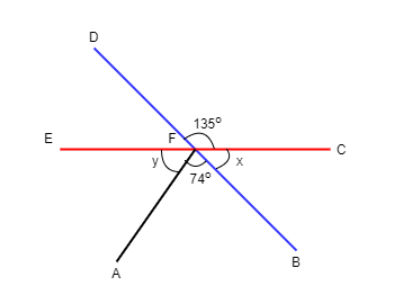
In the figure (not drawn to scale), EFC and DFB are straight lines. Find $\angle x$ and $\angle y$ respectively.

(A). ${40^ \circ },{62^ \circ }$
(B). ${45^ \circ },{61^ \circ }$
(C). ${47^ \circ },{54^ \circ }$
(D). ${30^ \circ },{60^ \circ }$

Answer 1

Hint: Use the property of straight lines that the sum of all angles formed on one side of it is \[{180^ \circ }\], Now consider DFB to calculate $x$ first and then use EFC to calculate the value of $y$.

Complete step-by-step answer:
According to the given information we know that DFB and EFC is a straight line
We have angle DFC = \[{135^ \circ }\] and angle AFB = \[{74^ \circ }\]
Since we know that DFB is a straight line so by the property of straight line sum of angles that are formed on the straight line is \[{180^ \circ }\]
Therefore $\angle $DFC + $\angle $BFC = \[{180^ \circ }\]
Substituting the given value in the above equation
\[{135^ \circ }\] + $\angle $x = \[{180^ \circ }\]
$ \Rightarrow $$\angle $x = \[{180^ \circ }\] – \[{135^ \circ }\]
$ \Rightarrow $$\angle $x = ${45^ \circ }$
As we know that since the EFC is a straight line so by the property of straight line sum of angles that are formed on the straight line is \[{180^ \circ }\]
Therefore $\angle $y + $\angle $AFB + $\angle $x = \[{180^ \circ }\]
Substituting the given values in the above equation
$\angle $y + \[{74^ \circ }\] + ${45^ \circ }$ = \[{180^ \circ }\]
$ \Rightarrow $$\angle $y = \[{180^ \circ }\]– \[{119^ \circ }\]
$ \Rightarrow $$\angle $y = ${61^ \circ }$
So the value of angles$\angle $x and $\angle $y are${45^ \circ }$, ${61^ \circ }$
Hence option B is the correct option.

Note: In the above solution we used one of the properties of line but there are more properties shown by straight lines but before that let’s discuss what is a straight line? A line is a projection which is not bend or curved at any point from start point and end point of line this is called straight line the properties shown by straight lines are that a straight line have only one dimension it can be horizontal, diagonal or vertical in position, both ends of a straight line can be extend to an infinite distance.