Question

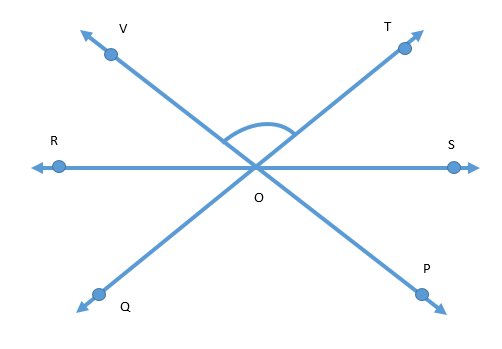
In the figure line RS, VP and TQ intersect in point O, $\angle VOS = {100^ \circ }$ and $\angle ROT = {120^ \circ }$. Find $\angle ROQ,\angle QOP$ and $\angle POS$.

Answer 1

Hint: We will first introduce the concept of vertically opposite angles and then term all the vertically opposite angles pair in this figure and then sum two among them according to the given data in the question and thus on modifying have the required answer.

Complete step-by-step answer:
In the figure, we are already given that RS, VP and TQ intersect in point O.
$ \Rightarrow \angle ROV = \angle POS$ (Vertically opposite angles) ……………(1)
\[ \Rightarrow \angle ROQ = \angle SOT\] (Vertically opposite angles) ……………(2)
\[ \Rightarrow \angle VOT = \angle QOP\] (Vertically opposite angles) ……………(3)
Now we are already given that: \[\angle ROT = {120^ \circ }\;\] and \[\angle VOS = {100^ \circ }\;\].
We can clearly see that: \[\angle ROT = \angle ROV + \angle VOT\]
By using (1), we can write the above expression as:
\[ \Rightarrow \angle ROT = \angle POS + \angle VOT\]
Now, since \[\angle ROT = {120^ \circ }\;\].
\[ \Rightarrow \angle POS + \angle VOT = {120^ \circ }\;\] …………..(4)
Since, we can see that PV is a straight line.
$ \Rightarrow \angle VOT + \angle TOS + \angle SOP = {180^ \circ }$
Now using (4) in above expression, we will get:-
$ \Rightarrow \angle TOS + {120^ \circ } = {180^ \circ }$
Simplifying the expression further to get:-
$ \Rightarrow \angle TOS = {60^ \circ }$ ……………(5)
Now, putting this in (2), we will get:-
\[ \Rightarrow \angle ROQ = {60^ \circ }\] ……………..(A)
Also, we can observe that: \[\angle VOS = \angle VOT + \angle TOS\]
By using (5) and given $\angle VOS = {100^ \circ }$, we can write the above expression as follows:
\[ \Rightarrow {100^ \circ } = \angle VOT + {60^ \circ }\]
Simplifying it further to get the following expression:-
\[ \Rightarrow \angle VOT = {40^ \circ }\]
Now, using (3), we will get:-
\[ \Rightarrow \angle QOP = {40^ \circ }\] …………..(B)
Now, since RS is a straight line. We will get the following expression:-
$ \Rightarrow \angle ROQ + \angle QOP + \angle POS = {180^ \circ }$
Now using (A) and (B) in above expression, we will get:-
$ \Rightarrow {100^ \circ } + \angle POS = {180^ \circ }$
Simplifying the expression further to get:-
$ \Rightarrow \angle POS = {80^ \circ }$ ……………(C)

$\angle ROQ = {60^ \circ }, \angle QOP = {40^ \circ } \text{and} \angle POS = {80^ \circ }$.

Note: The students must keep in mind that the angle on a straight line is known as straight angle and it is always equal to ${180^ \circ }$. The angles combining to form such angles are known as linear or supplementary angles.
The students must also know that vertically opposite angles are the angles which are opposite to each other when two or more lines cross. These angles are always equal. Here, in this question above, we have used the concept of vertically opposite angles only.