Question

In the figure, line \[l\] is parallel to the line \[m\], and line \[p\] is the transversal. Find the measure of \[x\].

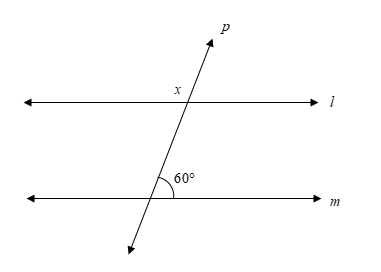
Answer 1

Hint: Here, we need to find the measure of the angle \[x\]. We will use the property of alternate interior angles and linear pair angles to find the measure of the angle \[x\]. The alternate interior angles on the opposite sides of a transversal, intersecting two parallel lines, are equal.

Complete step-by-step answer:
First, we will mark another angle in the given figure.

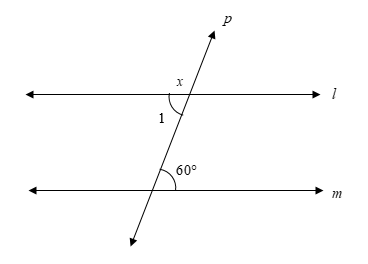
We will use the property of alternate interior angles and linear pair angles to find the measure of the angle \[x\].
It is given that line \[l\] is parallel to the line \[m\], and line \[p\] is the transversal.
Therefore, we get the alternate interior angles
\[\angle 1 = 60^\circ \]
Now, we will use the property of angles lying on a line, that is forming a linear pair.
From the figure, we can observe that the required angle \[x\] and angle 1 form a linear pair.
Therefore, we get
\[ \Rightarrow x + \angle 1 = 180^\circ \]
Substituting \[\angle 1 = 60^\circ \] in the equation, we get
\[ \Rightarrow x + 60^\circ = 180^\circ \]
Subtracting \[60^\circ \] from both sides of the equation, we get
\[ \Rightarrow x + 60^\circ - 60^\circ = 180^\circ - 60^\circ \]
Thus, we get
\[\therefore x = 120^\circ \]

Therefore, we get the measure of angle \[x\] as \[120^\circ \].

Note: We can also solve the problem using co-interior angles and vertically opposite angles.
Let the vertically opposite angle to the angle \[x\] be angel 2.
Co-interior angles are the angles which lie between two lines and are on the same side of the transversal.
It is given that line \[l\] is parallel to the line \[m\], and line \[p\] is the transversal.
Therefore, angle 2 and the given angle of measure \[60^\circ \] form co-interior angles.
The sum of co-interior angles between two parallel lines is always equal to 180 degrees.
Thus, we get
\[ \Rightarrow 60^\circ + \angle 2 = 180^\circ \]
Subtracting \[60^\circ \] from both sides of the equation, we get
\[ \Rightarrow \angle 2 = 120^\circ \]
Now, the vertically opposite angles formed at the point where two lines intersect, are always equal.
Therefore, we get
\[\therefore x = 120^\circ \]
Therefore, we get the measure of angle \[x\] as \[120^\circ \].