Question

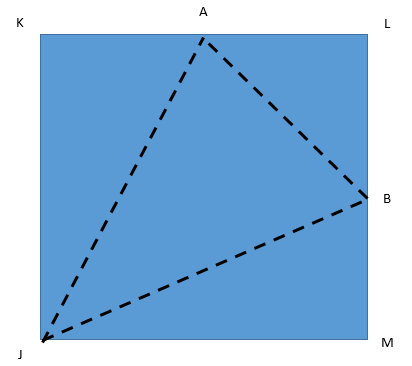
In the figure, JKLM is a square with sides of length 6 units. Point A and B are the mid – points of the sides KL and LM respectively. If a point is selected at random from the interior of the square, what is the probability that the point will be chosen from the interior of \[\vartriangle JAB\]?

Answer 1

Hint: We will basically divide the area of the triangle JAB by the area of the square JKLM and that will be the answer and now to find the area of the square, we will use the formula for area of squares. Now, for the area of the triangle, we will find the areas of the rest of triangles KJA, BMJ and ABL and subtract it from the square and thus have the answer.

Complete step-by-step answer:
We know that area of a square is given by the formula:-
$ \Rightarrow Area = {(Side)^2}$
Now, put inside 6 units as given in the question. We will then get:-
Area of the square JKLM = ${(6)^2} = 36$ square units. ……………..(1)
Now, we know that the area of triangle is given by the following formula:-
$ \Rightarrow Area = \dfrac{1}{2} \times b \times h$, where b is the base of the triangle and h is the height of the triangle.
Now, we will find the areas of three triangles which are KJA, BMJ and ABL.
So, area of triangle KJA is given by:-
$ \Rightarrow $Area of $\vartriangle KJA$ = $\dfrac{1}{2} \times AK \times KJ$
Now, since A is the mid – point, so, AK = 3 units and KJ = 6 units (already given)
$\therefore $Area of $\vartriangle KJA$ = $\dfrac{1}{2} \times 3 \times 6$
Simplifying it to get:-
$ \Rightarrow $Area of $\vartriangle KJA$ = 9 square units. …………..(2)
Similarly, the area of triangle BMJ is also 9 square units. …………..(3)
Now, we need to find the area of the triangle ALB.
$ \Rightarrow $Area of $\vartriangle ALB$ = $\dfrac{1}{2} \times AL \times LB$ (AL = LB = 3 units)
Simplifying by putting in the values to get:-
$ \Rightarrow $Area of $\vartriangle ALB = \dfrac{9}{2}$ square units. …………..(4)
Since, we see that $ar(\vartriangle KAJ + \vartriangle JMB + \vartriangle ALB + \vartriangle JAB) = ar(\square JKLM)$
Putting values in this expression from the equations (1), (2), (3) and (4) to get:-
$ \Rightarrow ar(\vartriangle JAB) + 9 + 9 + \dfrac{9}{2} = 36$
Simplifying the values by rearranging the terms to get:-
$ \Rightarrow ar(\vartriangle JAB) = \dfrac{{27}}{2}$ square units ……………..(5)
Now, we will use the formula of probability which states that the probability of an event is the favorable
Event divided by the total.
$\therefore \text{Probability} = \dfrac{{ar(\vartriangle JAB)}}{{ar(\square JKLM)}}$
Putting in the values from (1) and (5) to get:-
$\therefore \text{Probability} = \dfrac{{\dfrac{{27}}{2}}}{{36}}$
Simplifying to get:-
$\therefore \text{Probability} = \dfrac{3}{8}$

Hence, the answer is $\dfrac{3}{8}$.

Note: The students must wonder that we have the formula of area of triangle as $Area = \dfrac{1}{2} \times b \times h$, where b is the base of the triangle and h is the height of the triangle. If we carefully look at it, it is just half the area of what a rectangle has. Why is it so? Let us understand this in brief detail.
If you join the triangle with the same triangle by inverting it, you will get a rectangle so the length is the same as the base and breadth is the same as the height of the triangle. So, a triangle is basically half of the rectangle. This is the reason for this formula.
Probability helps in many aspects in our real life. For example: If you have to appear for any competitive exam, then you will know what are your chances to pass through that by calculating the probability by dividing the number of seats by the number of aspirants.