Question

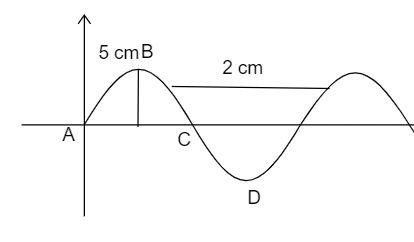
In the figure, it is given that the wave of frequency $100\,Hz$ is produced in the string. Find its amplitude, wavelength, velocity and nature of the wave.

Answer 1

Hint: Amplitude is the maximum height of the wave that is either in its crest or trough of the wave. Frequency of the wave is the number of waves passing through a particular point in a given time. From the given graph, find the value of the amplitude and the frequency of the wave. Use the formula of the velocity given below and substitute the value of the frequency and the frequency in it to obtain the value of the velocity of the wave.

Formula used:
The velocity of the wave is given by
$v = f \times \lambda $
Where $v$ is the velocity of the wave, $f$ is the frequency of the wave and $\lambda $ is the wavelength of the wave.

Complete step by step answer:
Frequency of the wave, $f = 100\,Hz$
(a) From the given figure, it is clear that the amplitude of the wave, that is the height at which the peak point of the wave ends is observed as $5\,cm$.
(b) Frequency is the distance between the waves. It is also said as the number of waves that pass a fixed place in a given time. From the graph it is observed as $20\,cm$ .
(c) In order to find the velocity of the given wave, use the formula given above.
$v = f \times \lambda $
Substitute the known values in the above equation,
$v = 100 \times 0.2$
By doing the multiplication in the right hand side of the above equation.
$v = 20\,m{s^{ - 1}}$

Hence, The velocity of the wave is obtained as $20\,m{s^{ - 1}}$.

Note: Remember that the wavelength is the length of the one wave and the amplitude is the height of the crest of one wave. The sinusoidal wave possesses wave regions in both up and down the axis, however the amplitude is taken at the top of the axis.