Question

In the figure, if $QP||SR$ , the value of $a$ is

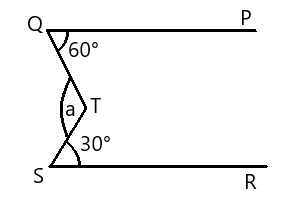
a) $40^\circ $
b) $30^\circ $
c) $90^\circ $
d) $80^\circ $

Answer 1

Hint: Here in this question we can see that we have been given a figure and we are given the angles of some parts. We have been given that $QP||SR$ . So we will first construct a line going through the middle such that all the three lines will be parallel to each other. So we will take the line as $LM$ , and we will draw it such that $LM||PQ||SR$ .

Complete answer:
Here we have been given $\angle PQT = 60^\circ $ and we have another angle $\angle TSR = 30^\circ $ .
Let us draw a line $LM$ parallel to $PQ$ and $SR$ .
Here is the diagram below:

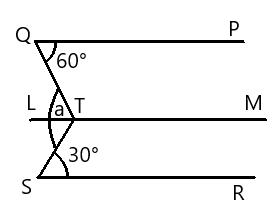
From the diagram we can see that we have line $LM$ parallel to $QP$ and the other line $QT$ is a transversal.
We know that in parallel lines alternate angles are equal.
From the diagram, we can see that
 $\angle LTQ = \angle PQT = 60^\circ $ , because these are alternate angles.
Therefore we have $\angle LTQ = 60^\circ $
Now we can see that $LM$ is also parallel to \[SR\] and $TS$ is a transversal.
So we can write that
 $ \Rightarrow \angle TSR = \angle LTS = 30^\circ $
Therefore we have another angle
$ \Rightarrow \angle LTS = 30^\circ $
We have to find the value of $\angle QTS = a$ , we can write this angle as the sum of two angles i.e.
$ \Rightarrow \angle QTS = \angle QLT + \angle LTS$
Therefore, we will now substitute the value of angles in the above equation and we have
$ \Rightarrow a = 60^\circ + 30^\circ $
It gives us value
$ \Rightarrow a = 90^\circ $

Therefore, the correct option is C

Note: We should know that when two or more lines are separated at an equidistant and never coincide then we can say that the lines are parallel as in the above question, we have lines $LM||PQ||SR$ . But it should be noted that a transversal line is the one that intersects either parallel lines or normal lines.