Question

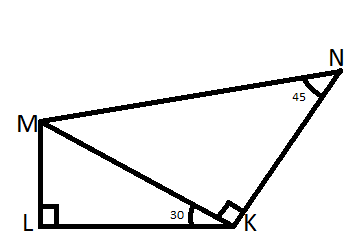
In the figure, if LK =$\sqrt 3 $, find MK, ML, KN, MN and find the perimeter of quadrilateral LMNK.

A. $6(2\sqrt 2 + 3 + \sqrt 3 )$
B. $6(3 + \sqrt 3 )$
C. $6(2\sqrt 2 + 3)$
D. $2\sqrt 2 + 3 + \sqrt 3 $

Answer 1

Hint – In order to solve this problem use trigonometric angles in triangles to get the length of all the sides and then calculate the perimeter by summing up all the sides.

Complete step-by-step answer:
Firstly we consider triangle LMK.
So, we can say that $\tan 30 = \dfrac{{LM}}{{LK}} = \dfrac{1}{{\sqrt 3 }}$.
The value of LK = $\sqrt 3 $(Given)
On putting the value of LK in above equation we get,
\[ \Rightarrow \dfrac{{LM}}{{\sqrt 3 }} = \dfrac{1}{{\sqrt 3 }}\]
We get LM = 1 ………………………….(1)
And we can also write $\sin 30 = \dfrac{{LM}}{{MK}}$.
On assigning value we get, $\sin 30 = \dfrac{1}{2} = \dfrac{1}{{MK}}$
So we got MK = 2 ………………………..(2)
Now, on considering triangle NKM.
We can say that $\tan 45 = 1 = \dfrac{{MK}}{{NK}} = \dfrac{2}{{NK}}$. (From (2))
So, we got NK = 2 ……………(3)
We can also do $\sin 45 = \dfrac{{MK}}{{MN}}$.
on assigning the values we got above equation as $\dfrac{1}{{\sqrt 2 }} = \dfrac{2}{{MN}}$
We got $MN = 2\sqrt 2 $ ……………..(4)
So, we got ${\text{MN}} = 2\sqrt 2 $, NK = 2, MK = 2, LM = 1.
So, the perimeter of quadrilateral LMNK is
LK + KN + NM + ML = $\sqrt 3 + 2 + 2\sqrt 2 + 1 = 3 + 2\sqrt 2 + \sqrt 3 $.
So, we got the perimeter as $3 + 2\sqrt 2 + \sqrt 3 $.
Hence the correct option is D.

Note – To solve such problems we need to calculate all the lengths of the given figure with the help of trigonometric functions tan and sin one can also use cos to calculate the lengths in place of sin. Then we have calculated the perimeter in this problem you should know that ${\text{tan30 = }}\dfrac{{\text{1}}}{{\sqrt {\text{3}} }}{\text{ = }}\dfrac{{{\text{perpendicular}}}}{{{\text{base}}}}{\text{,}}\,{\text{sin30 = }}\dfrac{{\text{1}}}{{\text{2}}}{\text{ = }}\dfrac{{{\text{perpendicular}}}}{{{\text{hypotenuse}}}}{\text{,}}\,{\text{and tan 45 = 1, sin45 = }}\dfrac{{\text{1}}}{{\sqrt {\text{2}} }}.$ knowing these values you can calculate everything asked in this problem.