Question

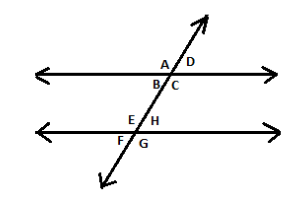
In the figure if line L$\parallel$M and line N is the transversal then find the value of A and B.

Answer 1

Hint: In this question we have to find the value of “a” and “b”. First of all, recall the relations among the angles formed when a transversal cuts two parallel lines. Consider the four angles formed by transversal “n” to line “l” be$\angle A,\angle B,\angle C,\angle D$. Whereas the line “m” be $\angle E,\angle F,\angle G,\angle H$.

Complete step-by-step answer:
When a transversal cuts two or more parallel lines, then the formed acute angles are congruent to each other while the obtuse angles are congruent to each other.
In Figure 2: -
$\angle A,\angle C;\angle B,\angle D;\angle E,\angle G;\angle F,\angle H$are vertically opposite to each other.
$\therefore \angle A = \angle C;\angle B = \angle D;\angle E = \angle G;\angle F = \angle H$
Therefore,
$\angle B = \angle D$
And according to question:$\angle B = {52^0}\& \angle D = a$
$\therefore a = {52^0}$
Again,
$\angle B,\angle E;\angle B,\angle H$are …… angles.
$\therefore $So, they are supplementary
i.e. $\angle B + \angle E = {180^0}$
$\angle B + \angle H = {180^0}$
According to question:
${
  \therefore \angle B = {52^0}\& \angle E = b \\
  \therefore {52^0} + b = {180^0} \\
  \therefore b = {128^0} \\
} $
${
  \therefore a = {52^0} \\
  b = {128^0} \\
} $

Note: There are many ways to solve such type of questions for example if there is any problem regarding interior angles, the simply find $\angle A$ by using $\angle A + \angle D = {180^0}$ [because ‘l’ is a straight line] and then use $\angle A = \angle E$ [because $\angle A,\angle E;\angle B,\angle F;\angle D,\angle H;\angle C,\angle G$ corresponding to each other].