
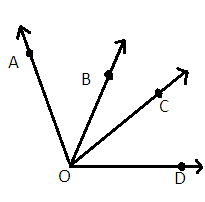
In the figure, If $\angle {\text{AOC = }}\angle {\text{BOD}}$, $\angle {\text{AOB = }}{45^ \circ }$ $\angle {\text{BOD = }}{60^ \circ }$ then find $\angle {\text{BOC}}$.

Answer
586.2k+ views
Hint: Use the given$\angle {\text{AOC = }}\angle {\text{BOD}}$. Then from observation of the diagram, we can write angle AOC to be the sum of angle AOB and angle BOC. Then put the value of angle AOC in the given$\angle {\text{AOC = }}\angle {\text{BOD}}$.Then put the given values of $\angle {\text{AOB}}$ and $\angle {\text{BOD}}$ in the equation formed and solve it to get $\angle {\text{BOC}}$.
Complete step-by-step answer:
Given, $\angle {\text{AOC = }}\angle {\text{BOD}}$ and $\angle {\text{AOB = }}{45^ \circ }$. Also $\angle {\text{BOD = }}{60^ \circ }$
Now we have to find $\angle {\text{BOC}}$.
We are given that,
$ \Rightarrow $ $\angle {\text{AOC = }}\angle {\text{BOD}}$-- (i)
From diagram it is clear that-
$ \Rightarrow $ $\angle {\text{AOB + }}\angle {\text{BOC = }}\angle {\text{AOC}}$ --- (ii)
Then substituting the values from eq. (ii) to eq. (i), we get,
$ \Rightarrow $ $\angle {\text{AOB + }}\angle {\text{BOC = }}\angle {\text{BOD}}$
On putting the values of $\angle {\text{AOB}}$ and $\angle {\text{BOD}}$, we get-
$ \Rightarrow 45 + \angle {\text{BOC = 60}}$
On transferring ${45^ \circ }$ from left side to right side, its sign changes and we get,
$ \Rightarrow \angle {\text{BOC = 60 - }}45$
On subtraction we get,
$ \Rightarrow \angle {\text{BOC = 15}}^\circ $
Hence $\angle {\text{BOC = 15}}^\circ $ .
Note: In this question, the student may get stuck if he or she writes$\angle {\text{BOD}} = \angle {\text{BOC + }}\angle {\text{COD}}$ in eq. (i) because we are not given the value of $\angle BOC$ and $\angle AOC$ in the question so split the angles into the only those angles whose value is given in the question, Otherwise the question cannot be solved. But if we were further asked to find $\angle COD$ then it will be easy to find as we have already obtained the value of $\angle COD$because now we know the value of $\angle BOC$ and the value of $\angle BOD$ is already given so just put the values in the equation-
$ \Rightarrow \angle {\text{BOD}} = \angle {\text{BOC + }}\angle {\text{COD}}$
We get,
$ \Rightarrow 60 = 15{\text{ + }}\angle {\text{COD}}$
Then on solving we get-
$ \Rightarrow \angle COD = 60 - 15 = 45$
So $\angle COD$= $\angle {\text{AOB = }}{45^ \circ }$
Complete step-by-step answer:
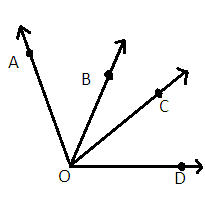
Given, $\angle {\text{AOC = }}\angle {\text{BOD}}$ and $\angle {\text{AOB = }}{45^ \circ }$. Also $\angle {\text{BOD = }}{60^ \circ }$
Now we have to find $\angle {\text{BOC}}$.

We are given that,
$ \Rightarrow $ $\angle {\text{AOC = }}\angle {\text{BOD}}$-- (i)
From diagram it is clear that-
$ \Rightarrow $ $\angle {\text{AOB + }}\angle {\text{BOC = }}\angle {\text{AOC}}$ --- (ii)
Then substituting the values from eq. (ii) to eq. (i), we get,
$ \Rightarrow $ $\angle {\text{AOB + }}\angle {\text{BOC = }}\angle {\text{BOD}}$
On putting the values of $\angle {\text{AOB}}$ and $\angle {\text{BOD}}$, we get-
$ \Rightarrow 45 + \angle {\text{BOC = 60}}$
On transferring ${45^ \circ }$ from left side to right side, its sign changes and we get,
$ \Rightarrow \angle {\text{BOC = 60 - }}45$
On subtraction we get,
$ \Rightarrow \angle {\text{BOC = 15}}^\circ $
Hence $\angle {\text{BOC = 15}}^\circ $ .
Note: In this question, the student may get stuck if he or she writes$\angle {\text{BOD}} = \angle {\text{BOC + }}\angle {\text{COD}}$ in eq. (i) because we are not given the value of $\angle BOC$ and $\angle AOC$ in the question so split the angles into the only those angles whose value is given in the question, Otherwise the question cannot be solved. But if we were further asked to find $\angle COD$ then it will be easy to find as we have already obtained the value of $\angle COD$because now we know the value of $\angle BOC$ and the value of $\angle BOD$ is already given so just put the values in the equation-
$ \Rightarrow \angle {\text{BOD}} = \angle {\text{BOC + }}\angle {\text{COD}}$
We get,
$ \Rightarrow 60 = 15{\text{ + }}\angle {\text{COD}}$
Then on solving we get-
$ \Rightarrow \angle COD = 60 - 15 = 45$
So $\angle COD$= $\angle {\text{AOB = }}{45^ \circ }$
Recently Updated Pages
Master Class 7 English: Engaging Questions & Answers for Success

Master Class 7 Maths: Engaging Questions & Answers for Success

Master Class 7 Science: Engaging Questions & Answers for Success

Class 7 Question and Answer - Your Ultimate Solutions Guide

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Trending doubts
What are the factors of 100 class 7 maths CBSE

The value of 6 more than 7 is A 1 B 1 C 13 D 13 class 7 maths CBSE

Convert 200 Million dollars in rupees class 7 maths CBSE

What were the major teachings of Baba Guru Nanak class 7 social science CBSE

Find the largest number which divides 615 and 963 leaving class 7 maths CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE





