Question

In the figure, if AB||CD, $\angle APQ={{50}^{o}}$ and $\angle PRD={{127}^{o}}$. Then find the values of ‘x’ and ‘y’.

Answer 1

Hint: First use the concept of alternate angles in a set of parallel lines to get the value of ‘x’. Then use the concept of sum of angles in a straight line to get the value of the third angle of the triangle, hence use the theory that the sum of angles of the triangle is ${{180}^{\circ }}$ to get the answer.

“Complete step-by-step answer:”
Now we know in the concept of pair lines there is a concept of alternate angles that is, if two lines let’s suppose WX and YZ are parallel to each other.

A transversal ST is drawn such that it cuts S at WX and T at YZ. Then we can say that angle WST and angle STZ is equal as they are alternate angles.
Now consider the given figure,

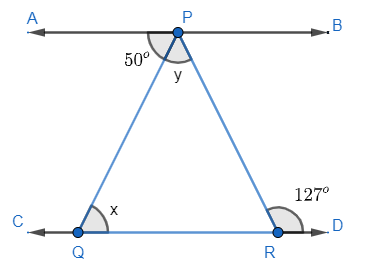
Here line AB is parallel to CD and PQ is traversal line, then as per alternate angles, $\angle PQR=\angle APQ$
As we know that the $\angle APQ={{50}^{\circ }}$ and $\angle PQR=x$, so we can say that
$x={{50}^{\circ }}..........(i)$
Now let’s suppose a triangle ABC is given and It’s one side BC is extended to D.

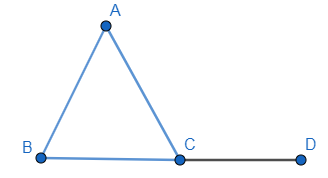
Now the sum of angles of the triangle is ${{180}^{\circ }}$, and the angle contained in a straight line is ${{180}^{\circ }}$.
So, now we can say,
$\angle ABC+\angle BCA+\angle CAB=\angle ACB+\angle ACD$
Hence we can say that,
$\angle ABC+\angle BAC=\angle ACD$
Now we can use this fact in the question and instead of triangle ABC, PAR will be taken so,
$\angle PQR+\angle QRP=\angle PRD$
Substituting the given values, i.e., $\angle PQR=x,\angle QPR=y,\angle PRD={{127}^{o}}$, so we can represent the above expression as
$x+y={{127}^{\circ }}$
Now substituting the value of ‘x’ from equation (i), we get
$\begin{align}
  & {{50}^{o}}+y={{127}^{\circ }} \\
 & \Rightarrow y={{127}^{o}}-{{50}^{o}}={{77}^{o}} \\
\end{align}$
Hence the value of x and y is ${{50}^{\circ }}$ and ${{77}^{\circ }}$ respectively.

Note: After finding the angle or value of x as ${{50}^{\circ }}$ we can find y by alternative method first getting the angle of PRQ using the fact angle in a straight line is ${{180}^{\circ }}$. Then we know two interior angles out of three in a triangle, so can use the concept that the sum of angles of the triangle is ${{180}^{\circ }}$ to get the answer.