Question

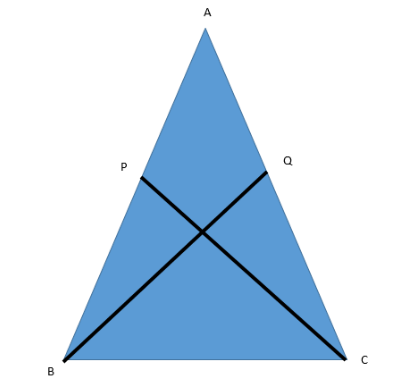
In the figure given below, P and Q are two points of equal side AB and AC of an isosceles triangle ABC such that AP = AQ, prove that BQ = CP.

Answer 1

Hint: We will first prove that BP = CQ. Now, using one corresponding angle of the triangles PBC and QCB, we will prove that these triangles are congruent and finally by using CPCT, we will show the required result.

Complete step-by-step answer:
We are already given that ABC is isosceles with AB = AC. …………(1)
We also know that angles opposite to equal sides are equal in a triangle.
Hence, \[\angle B = \angle C\] ……………(2)
We are given that the points P and Q are taken such that AP = AQ ………..(3)
Subtracting (3) from (1), we will get: AB – AP = AC – AQ …………..(4)
We can clearly see that AP + PB = AB and AQ + QC = AC
Using these equalities in (4), we will get: BP = CQ …………….(5)
Now, let us consider the triangles PBC and QCB.
In $\vartriangle PBC$ and $\vartriangle QCB$, we have:-
BP = CQ (By equation 5)
\[\angle B = \angle C\] (By equation 2)
BC = CB (Common line)
Hence, $\vartriangle PBC \cong \vartriangle QCB$. (By SSA congruence rule)
[If two triangles satisfy the SSA condition and the length of the side opposite the angle is greater than or equal to the length of the adjacent side (SSA, or long side-short side-angle), then the two triangles are congruent]
Hence, BQ = CP (By CPCT)

Note: The students might not know why the concept of CPCT works in congruent triangles. So, here is a brief overview about it. Congruence of two triangles basically means that they are exact replicas of each other with all corresponding angles and sides equal. In simpler words, it means that you can cover one triangle with another one without over or under shadowing it at all.
[CPCT stands for Corresponding parts of congruent triangles. CPCT theorem states that if two or more triangles which are congruent to each other are taken then the corresponding angles and the sides of the triangles are also congruent to each other]