Question

In the figure given below, l and m are two parallel tangents to a circle with center O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that $\angle DOE = {90^ \circ }$.
               

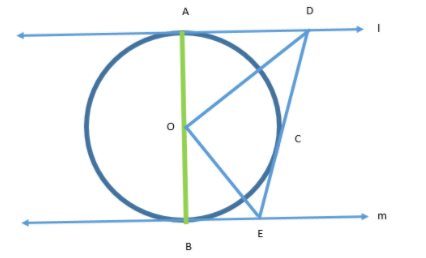
Answer 1

Hint: We will first join A and B, then prove the triangles ODA and OCD to be congruent and triangles OCE and OBE to be congruent and then consider the angles associated with line AB to get the required result.

Complete step-by-step answer:
Let us first join A and B as follows:
               

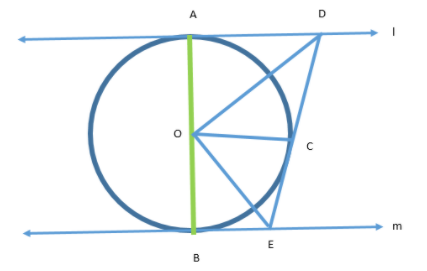
Now, let us consider $\vartriangle OAD$ and $\vartriangle OCD$:
OA = OC (Radii of the same circle)
OD = OD (Common)
AD = CD (Tangents from same external point are equal to each other)
(A line which touches a circle or ellipse at just one point is known as a tangent)
Hence, $\vartriangle OAD \cong \vartriangle OCD$ (By SSS property)
(The SSS rule states that: If three sides of one triangle are equal to three sides of another triangle, then the triangles are congruent.)
Therefore, $\angle AOD = \angle COD$ (BY CPCT) ………….(1)
(CPCT stands for Corresponding parts of congruent triangles. CPCT theorem states that if two or more triangles which are congruent to each other are taken then the corresponding angles and the sides of the triangles are also congruent to each other.)
Now, if we do the same process in $\vartriangle OBE$ and $\vartriangle OCE$, we will get:
$\vartriangle OBE \cong \vartriangle OCE$(By SSS property)
Now, using CPCT, we will get:- $\angle BOE = \angle COE$ ………….(2)
We are already given that O is the center and since AB passes through O and touches the boundary of the circle. Hence, AB is a diameter.
Hence, it is a straight line.
Therefore, \[\angle AOB = {180^ \circ }\]
We can rewrite it as:-
$\angle AOD + \angle DOC + \angle COE + \angle EOB = {180^ \circ }$
Now using (1) and (2), we can rewrite it as:-
$\angle COD + \angle DOC + \angle COE + \angle COE = {180^ \circ }$
$ \Rightarrow 2\angle COD + 2\angle COE = {180^ \circ }$
$ \Rightarrow 2(\angle COD + \angle COE) = {180^ \circ }$
$ \Rightarrow 2(\angle DOE) = {180^ \circ }$
$ \Rightarrow \angle DOE = {90^ \circ }$.
Hence, proved.

Note: The students must remember that they need to write the reasons for the equations they are using to prove some triangles congruent. Otherwise, the answer could be considered vague. Students must note that they need to prove that we have a straight line to use the sum of angles to be linear.