Question

: In the figure given below, $ \angle QSR $ is equal to

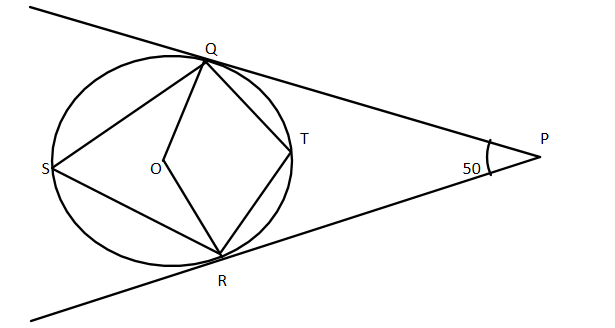
A. $ 65^\circ $
B. $ 50^\circ $
C. $ 70^\circ $
D. $ 75^\circ $

Answer 1

Hint:
Here we have the circle with the centre O and also have the tangents to this circle that are meeting at the point P and in the figure we need to find the value of the $ \angle QSR $
So here we will proceed by property that:
1) The line joining the centre of the circle and the point where the tangent meets the circle make the angle of $ 90^\circ $ with the tangent.
2) Angle subtended by an arc at the centre of the circle is twice the angle subtended at the circumference.

Complete step by step solution:
Here we need to just see the figure and apply the properties of the tangents and the circle in order to find the angle which is required.
Here we are given the figure as

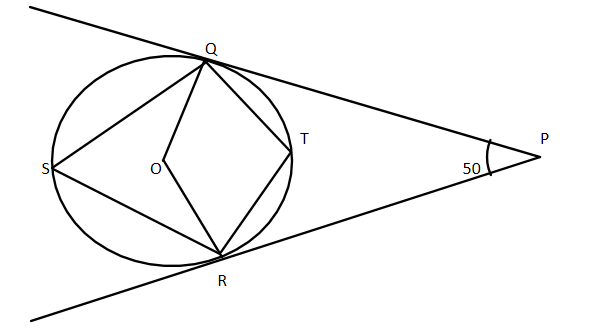
Here we have the circle with the centre O and also the tangents to this circle that are meeting at the point P and in the figure we need to find the value of the $ \angle QSR $
So we are given that $ \angle QPR = 50^\circ $
As we know that the line joining the centre of the circle and the point where tangent meets the circle make the angle of $ 90^\circ $ with the tangent.
Hence we can say that $ \angle QRP = \angle OQP = 90^\circ $
We know that $ ORPQ $ is a quadrilateral and the sum of all the angles of the quadrilateral is $ 360^\circ $
So we can say that
 $ \angle QPR + \angle QOR + \angle OQR + \angle ORP = 360^\circ $
Now substituting their values we get
 $
  50^\circ + \angle QOR + 90^\circ + 90^\circ = 360^\circ \\
  \angle QOR = 360 - 230 = 130^\circ \\
  $
Now we have got the angle subtended by the arc $ QTR $ at the centre of the circle but we need the angle subtended by this arc at the circumference at the point $ S $
We know the property of the circle that:
Angle subtended by an arc at the centre of the circle is twice the angle subtended at the circumference
So we can say that $ \angle QSR = \dfrac{{\angle QOR}}{2} = \dfrac{{130}}{2} = 65^\circ $

Hence we can say that A is the correct option.

Note:
Here a student need to remember all the properties of the circle and also the properties that the circle have with the tangents like:
1) The line joining the centre of the circle and the point where the tangent meets the circle make the angle of $ 90^\circ $ with the tangent.
2) Angle subtended by an arc at the centre of the circle is twice the angle subtended at the circumference.
3) Diameter of the circle is the largest chord and ends of any diameter of the circle, when joined with any point on the circumference, makes the angle of $ 90^\circ $
So these properties are to be remembered properly for solving such problems.