Question

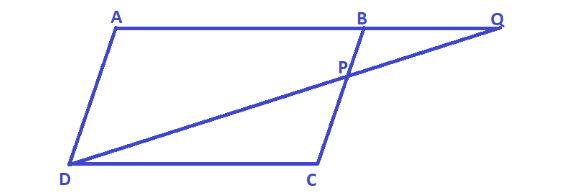
In the figure given below ABCD is a parallelogram. P is a point on BC such that \[{\text{BP:PC = 1:2}}\] , DP produced meets AB at Q. given the area if the triangle CPQ is equal to \[{\text{20c}}{{\text{m}}^2}\] . Calculate
A. Area of triangle CDP
B. Area of parallelogram ABCD

Answer 1

Hint: We will use the triangle similarity theorem to get the areas. For the first we will show the two triangles are similar using the tests of similarity. Then for finding the area of the parallelogram we will add the area of the lower triangle and the upper quadrilateral. Here also to find the area of the quadrilateral we will use the similarity of triangle theorem.

Complete step by step solution:
Given that,
ABCD is a parallelogram
 P is a point on BC such that \[{\text{BP:PC = 1:2}}\]

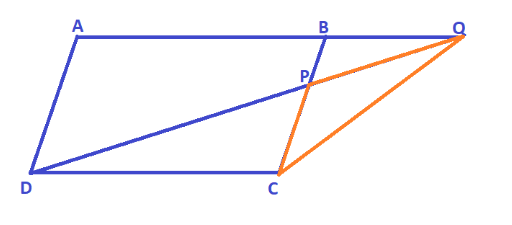
Now we will consider a pair of triangles.
 \[\vartriangle {{BPQ\& }}\vartriangle {\text{CPD}}\]

 \[\angle {\text{BPQ = }}\angle {\text{CPD}}........{\text{V}}{\text{.O}}{\text{.A}}\]
 \[\angle {\text{BQP = CDP}}.....{\text{alternate }}\angle {\text{s}}\]
 \[\therefore \vartriangle {\text{BPQ}} \sim \vartriangle {\text{CPD(by AA test )}}\]
Since triangles are similar,
 \[\dfrac{{BP}}{{CP}} = \dfrac{{PQ}}{{PD}} = \dfrac{{BQ}}{{CD}} = \dfrac{1}{2}(given\dfrac{{BP}}{{CP}} = \dfrac{1}{2})\]
Now since the triangles are similar the ratio of the areas of the triangles is equal to the square of ratio of the sides.
 \[\dfrac{{area\left( {\vartriangle {\text{BPQ}}} \right)}}{{area\left( {\vartriangle {\text{CPD}}} \right)}} = {\left( {\dfrac{{BP}}{{CP}}} \right)^2}\]
Putting the values from given data,
 \[
  \dfrac{{area\left( {\vartriangle {\text{BPQ}}} \right)}}{{area\left( {\vartriangle {\text{CPD}}} \right)}} = {\left( {\dfrac{1}{2}} \right)^2} \\
  \dfrac{{area\left( {\vartriangle {\text{BPQ}}} \right)}}{{area\left( {\vartriangle {\text{CPD}}} \right)}} = \dfrac{1}{4} \;
 \]
 \[\dfrac{{10}}{{area\left( {\vartriangle {\text{CPD}}} \right)}} = \dfrac{1}{4}\] [since \[area\left( {\vartriangle {\text{BPQ}}} \right) = \dfrac{1}{2} \times area\left( {\vartriangle CPQ} \right) = \dfrac{1}{2} \times 20 = 10c{m^2}\] ]
 \[area\left( {\vartriangle CDP} \right) = 10 \times 4\]
On multiplying we get,
 \[area\left( {\vartriangle CDP} \right) = 40c{m^2}\]
This is the solution for the first question.
Now we will jump on second.

 \[
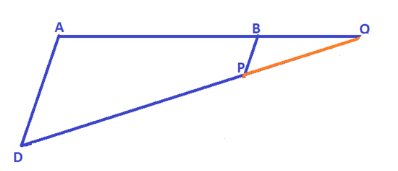
  \vartriangle AQD\& \vartriangle BQP \\
  \angle Q = \angle Q....common\angle \\
  \angle A = \angle B.....corresponding\angle \\
  \therefore \vartriangle AQD \sim \vartriangle BQP....\left( {{\text{byAAtest}}} \right) \;
 \]
Then the ratio of sides of similar triangles can be written as,
 \[\dfrac{{AQ}}{{BQ}} = \dfrac{{QD}}{{QP}} = \dfrac{{AD}}{{BP}}\]
BUT WE CAN OBSERVE THAT,
 \[QD = PQ + PD\]
So we can use \[\dfrac{{BP}}{{CP}} = \dfrac{{PQ}}{{PD}} = \dfrac{1}{2}\]
Then we can write,
 \[QD = PQ + PD = 1 + 2 = 3\]
 \[\dfrac{{AQ}}{{BQ}} = \dfrac{{QD}}{{QP}} = 3\]
This is the first step to be done.
 \[\dfrac{{area\left( {\vartriangle {\text{BPQ}}} \right)}}{{area\left( {\vartriangle AQ{\text{D}}} \right)}} = {\left( {\dfrac{{QP}}{{QD}}} \right)^2}\]
Putting the values here,
 \[\dfrac{{area\left( {\vartriangle {\text{BPQ}}} \right)}}{{area\left( {\vartriangle AQ{\text{D}}} \right)}} = {\left( {\dfrac{1}{3}} \right)^2}\]
Taking the squares we get,
 \[\dfrac{{area\left( {\vartriangle {\text{BPQ}}} \right)}}{{area\left( {\vartriangle AQ{\text{D}}} \right)}} = \dfrac{1}{9}\]
On cross multiplying we get,
 \[
  area\left( {\vartriangle AQ{\text{D}}} \right) = 9 \times area\left( {\vartriangle {\text{BPQ}}} \right) \\
  area\left( {\vartriangle AQ{\text{D}}} \right) = 9 \times 10 \\
  area\left( {\vartriangle AQ{\text{D}}} \right) = 90c{m^2} \;
 \]
We did all this work because,
 \[area\left( {ABCD} \right) = area\left( {ABPD} \right) + area\left( {\vartriangle CPD} \right)\]
Abd it is dependent on,
 \[area\left( {APBD} \right) = area\left( {\vartriangle AQD} \right) - area\left( {\vartriangle BPQ} \right)\]
Now we can write,
 \[area\left( {APBD} \right) = 90 - 10 = 80c{m^2}\]
And thus the area of the main parallelogram will be,
 \[area\left( {ABCD} \right) = area\left( {ABPD} \right) + area\left( {\vartriangle CPD} \right) = 80 + 40 = 120c{m^2}\]
So, the correct answer is “ \[120c{m^2}\] ”.

Note: Here just one thing is to be noticed and that is the theorems are the closest key to solve these types of geometrical problems. Using a single or two data values we can solve the problem. But here to use the theorem the two triangles must be similar. Also note that to find the area of a triangle we always don’t need height and base values.