Question

In the figure given below, AB is parallel to CD. What is \[\angle XOY\]?

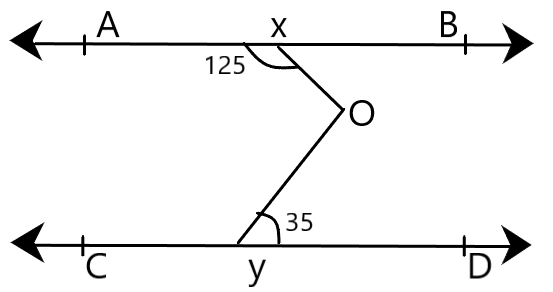
Answer 1

Hint: According to the given question, AB is parallel to CD. The given angle \[\angle AXO\] is given as \[{125^ \circ }\], and \[\angle OYD\] is given as \[{35^ \circ }\]. In order to solve this question, we need to find out complementary angles.

Complete step-by-step solution:
So, to get the solution to this question in a very simple way, we need to first construct a line \[OZ\]. After construction, we get:

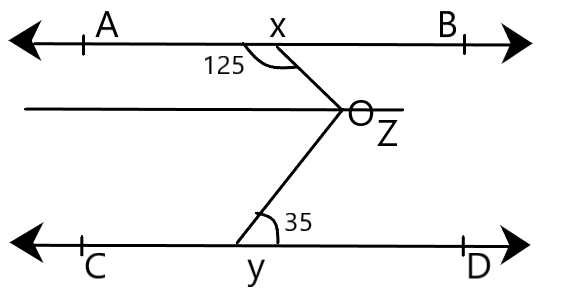
Now, we can see in the above figure that:
\[\angle XOZ = \angle BXO\], because the angles are alternate angles
Thus, \[\angle XOZ = \angle BXO = {180^ \circ } - {125^ \circ } = {65^ \circ }\], because the angles are linear angles
Also, \[\angle ZOY = \angle OYD = {35^ \circ }\], because\[\angle ZOY\] and \[\angle OYD\]are alternate angles
Therefore, \[\angle XOY = \angle XOZ + \angle ZOY = {65^ \circ } + {35^ \circ } = {100^ \circ }\]
Additional information: In Mathematics, Geometry is the branch that helps us study about angles, shape, sizes, and dimensions of certain objects or things. Depending upon dimensions there are two types of shapes, one is 2D shapes and other is 3D shapes.

Note: A pair of angles whose sum is 90 degrees are called complementary angles and when that pair of angles has sum of 180 degrees, then they are called supplementary angles. Often note that the angles occur in pairs when talking about complementary angles. In addition to it, one angle is a complement of the other angle.