Question

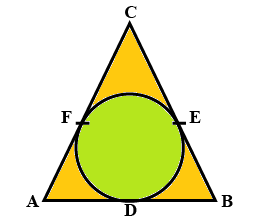
In the figure given below, a circle inscribed in triangle ABC touches its sides AB, BC and CA at the points D, E and F respectively. If AB = 12 cm, BC = 8 cm and AC = 10 cm, then find the lengths of AD, BE and CF.

Answer 1

Hint: We will use the fact that: Tangents from the same external points are equal in length. Using the fact, we will have some equations for the sides for the triangle then using those equations and the lengths mentioned in the question, we will have our answer.

Complete step-by-step answer:
We see that AC and AB touch the circle at F and D respectively and nowhere else.
Hence, we can call AC and AB the tangents to the circle.
Because tangent is a straight line or plane that touches a curve or curved surface at a point, but if extended does not cross it at that point.
Now, we will use the fact that: Tangents from the same external points are equal in length.
Now tangents AC and AB cut at F and D respectively coming from the same point A.
Hence, \[AF{\text{ }} = {\text{ }}AD\]
Similarly using the same argument again and again, we will have:-
\[BD{\text{ }} = {\text{ }}BE\]
\[CF{\text{ }} = {\text{ }}CE\]
Now, let \[AF = AD = x\] ……..(1)
\[BD = BE = y\] ……..(2)
\[CF = CE = z\;\] ……..(3)
We are already given in the question that AB = 12 cm, BC = 8 cm and AC = 10 cm.
We can clearly see in the figure that \[AB = AD + DB\].
Now, using (1) and (2) in this and the length of AB, we have:-
$ \Rightarrow 12 = x + y$ ……….(4)
We can clearly see in the figure that \[BC = BE + EC\].
Now, using (2) and (3) in this and the length of BC, we have:-
$ \Rightarrow 8 = y + z$ ……….(5)
We can clearly see in the figure that \[AC = AF + FC\].
Now, using (1) and (3) in this and the length of AC, we have:-
$ \Rightarrow 10 = x + z$ ……….(6)
Subtracting (5) from (4), we will have:-
$ \Rightarrow 4 = x - z$ ……..(7)
Adding both (6) and (7), we will get:-
$ \Rightarrow 14 = 2x$
$ \Rightarrow x = 7$ …….(8)
Putting this value of $x$ in (4), we get:-
$ \Rightarrow 12 = 7 + y$
$ \Rightarrow y = 5$ ………(9)
Putting (8) in (6), we get:-
$ \Rightarrow 10 = 8 + z$
$ \Rightarrow z = 2$ ………(9)
Now, we required the lengths of AD, BE and CF.
From (1), (2), (3), (8), (9) and (10), we have:-
\[AD = x = 7cm\]
\[BE = y = 5cm\]
\[CF = z\; = 2cm\]

Note: The students might forget to write the units at the end, but without unit we cannot talk about the concept of length. Writing just 5 does not make any sense, but 5 cm does.
The students might think that D, E and F are the midpoint but that is not necessary and you cannot put that argument without any solid reason as well.