Question

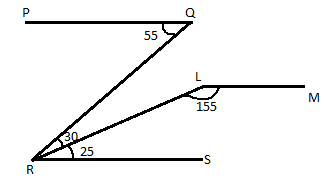
In the figure given above, PQ is parallel to RS. What is the angle between the lines PQ and LM?

Answer 1

Hint: In order to find the angle between two lines PQ and LM, we will use the sum of interior angle property which states that if a transversal line intersects two parallel lines, then each pair of co-interior angles is supplementary and vice- versa.

Complete step-by-step solution -

Given $PQ||RS$
Since, $PQ||RS$
By applying alternate angle property
$
  \angle PQR = \angle QRS = {55^0}..............\left( 1 \right) \\
  {\text{and }}\angle MLR + \angle SRL = {180^0} \\
$
Therefore, $LM||RS..............\left( 2 \right)$
(sum of interior angle property)
Therefore, from equation (1) and (2)
$PQ||RS$
Therefore, from sum of interior angle property the angle between the lines $PQ{\text{ and }}LM = {180^0}.$

Note: In order to solve these types of problems, learn all the properties of angles and parallel lines. Some of these properties are alternate angle property, corresponding angle property, vertically opposite angles etc. Also remember that the sum of interior angles of a triangle is 180 degrees while that of the sum of interior angles of squares is 360 degrees.