Question

In the figure, from the top of a solid cone of height $12cm$ and base radius $6cm$, a cone of height $4cm$ is removed by a plane parallel to the base. Find the total surface area of the remaining solid. (Use $\pi = \dfrac{{22}}{7}$ and $\sqrt 5 = 2.236$)

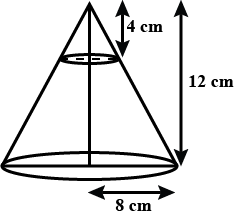
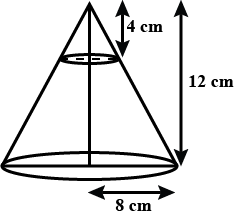
Answer 1

Hint: In this question the concept of Angle Angle Similarity theorem i.e. is a shortcut of showing that two triangles are similar and the formula of total surface area i.e. $ = \pi \left( {{R_1} + {R_2}} \right)l + \pi \left( {{R_1}^2 + {R_1}^2} \right)$ will be used.

Complete step-by-step answer:

According to the question it is given that a height and a base radius of the cone is given i.e. $12cm$ and $6cm$ respectively.
Here , from the diagram we can see $\Delta OAB$ and $\Delta OCD$ are similar so we will use $Angle Angle$ Similarity here that is the Third Angle Theorem states if two angles are congruent to two angles in another triangle, the third angles are congruent too.
Hence, $\Delta OAB \sim \Delta OCD$ [By $Angle Angle$ similarity]
$
   \Rightarrow \dfrac{{OA}}{{OC}} = \dfrac{{AB}}{{CD}} \\
   \Rightarrow AB = \dfrac{{4 \times 6}}{{12}} = 2cm \\
 $


Now, total surface of frustum $ = \pi \left( {{R_1} + {R_2}} \right)l + \pi \left( {{R_1}^2 + {R_1}^2} \right)$
$
   = \pi \left[ {\left( {{R_1} + {R_2}} \right)\sqrt {{{\left( {{R_1} - {R_2}} \right)}^2} + h} + {R_1}^2 + {R_2}^2} \right] \\
   = \dfrac{{22}}{7}\left[ {\left( {6 + 2} \right)\sqrt {{{\left( {6 - 2} \right)}^2} + {8^2}} + {6^2} + {2^2}} \right] \\
   = \dfrac{{22}}{7}\left[ {8 \times 4\sqrt 5 + 36 + 4} \right] \\
   = \dfrac{{22}}{7}\left[ {32 \times 2.236 + 40} \right] \\
   = 350.59c{m^2} \\
$
Hence the total surface area of the remaining solid is $350.59c{m^2}$.

Note: It is always advisable to remember the basic theorems and some formulas while involving shapes questions as it saves a lot of time . Eventually it will be difficult to mug up every concept but with time things get easier.