Question

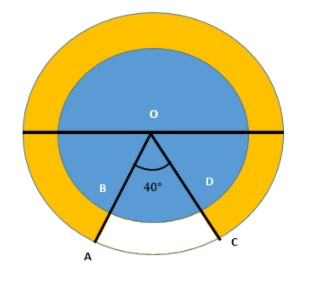
In the figure, find the area of the region in yellow color, enclosed between two concentric circles of radii 7 cm and 14 cm where $\angle AOC = {40^ \circ }$. Consider \[\pi = \dfrac{{22}}{7}\] .

Answer 1

Hint:We will first find the area of the bigger circle and subtract the area of the smaller circle from it. Now, we will find the area of sector of bigger circle with $\angle AOC = {40^ \circ }$ and subtract the area of sector of smaller circle from it and subtract the resultant from the resultant of difference of areas of complete circle, we will get the answer.

Complete step-by-step answer:
Let us first discuss the formulas we are going to use that is the area of a circle and area of sector.
Area of a circle is given by $A = \pi {r^2}$, where r is the radius of the circle.
Area of a sector is given by $A = \dfrac{\theta }{{{{360}^ \circ }}} \times \pi {r^2}$.
Now, let us say that ${r_1} = 7$ and ${r_2} = 14$.
So, let us find the area of the space which lies in a bigger circle but not in a smaller circle.
Area will be given by ${A_1} = \pi {r_2}^2 - \pi {r_1}^2$ which can be written as:-
${A_1} = \pi ({r_2}^2 - {r_1}^2)$
Now, we will use the formula of ${a^2} - {b^2} = (a - b)(a + b)$
Hence, we have:- ${A_1} = \pi ({r_2} - {r_1})({r_2} + {r_1})$
Now, putting in all the values, we will get:-
${A_1} = \dfrac{{22}}{7}(14 - 7)(14 + 7)$
Simplifying it, we will get:-
${A_1} = \dfrac{{22}}{7} \times 7 \times 21 = 22 \times 21 = 462c{m^2}$
Hence, ${A_1} = 462c{m^2}$ ………(1)
Now, let us find the area which we need to subtract from (1) that is the difference of area of sectors of both the circles. We will get:-
${A_2} = \dfrac{\theta }{{{{360}^ \circ }}} \times \pi {r_2}^2 - \dfrac{\theta }{{{{360}^ \circ }}}\pi {r_1}^2$
Rearranging the terms to get:-
${A_2} = \dfrac{\theta }{{{{360}^ \circ }}} \times \pi ({r_2}^2 - {r_1}^2)$
Now, we will use the formula of ${a^2} - {b^2} = (a - b)(a + b)$. So, we will get:-
${A_2} = \dfrac{\theta }{{{{360}^ \circ }}} \times \pi ({r_2} - {r_1})({r_2} + {r_1})$
Now, putting in all the values, we will get:-
${A_2} = \dfrac{{{{40}^ \circ }}}{{{{360}^ \circ }}} \times \dfrac{{22}}{7}(14 - 7)(14 + 7)$
Simplifying it:
${A_2} = \dfrac{1}{9} \times \dfrac{{22}}{7} \times 7 \times 21 = \dfrac{{154}}{3}c{m^2}$ ……….(2)
Now subtracting (2) from (1) will give us the required yellow region area.
Hence Area required = $\left( {462 - \dfrac{{154}}{3}} \right)c{m^2}$ that is equivalent to $\left( {\dfrac{{1232}}{3}} \right)c{m^2}$.

Note:The students must remember to put in the value of $\pi $ as $\dfrac{{22}}{7}$ as asked in question because using 3.14 may change the values required to us.Students should remember the definitions and formulas of area of circle and area of sector for solving these types of problems.