Question

In the figure, \[\Delta AHK\] is similar to \[\Delta ABC\]. If AK – 10 cm, BC – 3.5 cm and HK – 7 cm. Find AC?

Answer 1

Hint: In this question, we know that in similar triangles, the ratio of their corresponding sides are equal. So write the ratio of the corresponding sides of \[\Delta AHK\] and \[\Delta ABC\] and equate them. Then substitute the given values to get the value of AC.

Complete step-by-step answer:
We are given that, \[\Delta AHK\] is similar to \[\Delta ABC\]. So, if AK = 10 cm, BC = 3.5 cm and HK = 7 cm, we have to find the value of the side AC.

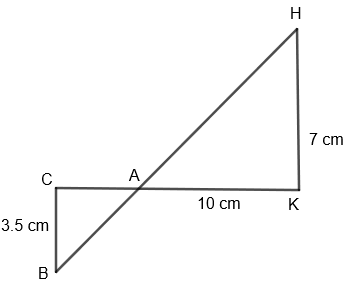
Before proceeding with this question, let us first see what similar triangles are. Two triangles are similar if their corresponding angles are equal and corresponding sides are in proportion. In other words, similar triangles are of the same shape, but not necessarily the same size. The sides of the two similar triangles are proportional. That is, if \[\Delta UVW\] is similar to \[\Delta XYZ\], then,

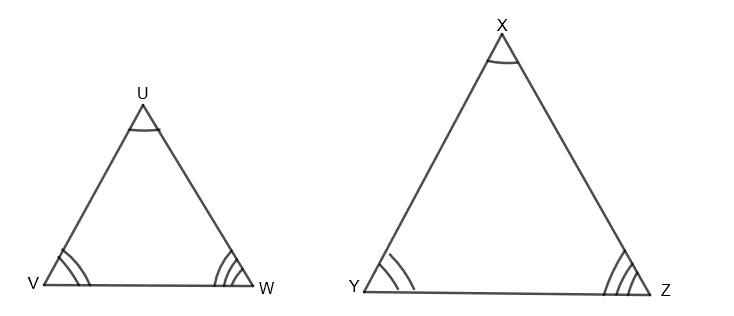
\[\dfrac{UV}{XY}=\dfrac{UW}{XZ}=\dfrac{VW}{YZ}\]
Let us consider the information given in the question.
 

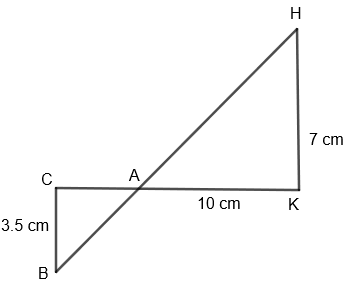
We know that when triangles are similar, the ratio of their corresponding sides are also equal. We are given that \[\Delta ABC\] is similar to \[\Delta AHK\]. So, the ratio of corresponding sides of these two triangles would be similar. So, we get,
\[\dfrac{AB}{AH}=\dfrac{AC}{AK}=\dfrac{BC}{HK}\]
We are given that BC = 3.5 cm, AK = 10 cm and HK = 7 cm. So by substituting these values in the above equation, we get, \[\dfrac{AC}{10}=\dfrac{3.5}{7}\]

Now, by cross multiplying the above equation, we get,
\[7AC=10\times 3.5\]
\[\Rightarrow 7AC=35\]
By dividing 7 on both the sides of the equation, we get,
\[AC=\dfrac{35}{7}\]
\[\Rightarrow AC=5cm\]
So, we get the value of AC as 5 cm.

Note: In the questions involving similar triangles, students often make mistakes in writing corresponding sides, that is, in our question some students may take BC corresponding to AK which is wrong. Here, side AC is corresponding to side AK, side HK to side BC, and side AB to side AH. Also, students must remember that in similar triangles, the ratio of the sides is equal, not the side itself like in congruent triangles.