Question

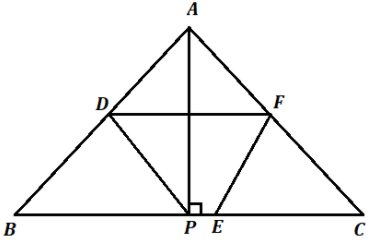
In the figure, DEF are midpoints of sides AB, BC and AC respectively. P is the foot of the perpendicular from A to side BC. Show that points D, F, E and P are concyclic.

Answer 1

Hint: To prove the points E, F, D and P are concyclic, we should consider \[\Delta \] ABC, quadrilateral BEFD and \[\Delta \] ABP and find the required data and then we should prove the quadrilateral PDFE is a cyclic quadrilateral.

Complete step-by-step solution:
Given : In \[\Delta \] ABC, D,E and F are the mid points of sides AB, BC, CA respectively. AP \[\bot \] BC.
To prove : E, F, D and P are concyclic.
Proof :
In \[\Delta \] ABC, D and F are mid points of AB and CA respectively.
\[\therefore \] DF || BC from mid point theorem
Similarly, EF || AB and ED || CA
In quadrilateral BEFD,
BE || DF and EF || BD with DF || BC and EF || AB
\[\therefore \]Quadrilateral BEFD is a parallelogram.
Similarly, quadrilateral ADEF is a parallelogram.
\[\therefore \] \[\angle \]A = \[\angle \]DEF since the opposite sides of parallelogram are equal
ED || AC and EC is the transversal,
\[\therefore \] \[\angle \]BED = \[\angle \]C as they are corresponding angles
\[\angle \]DEF = \[\angle \]DED + \[\angle \]DEF = \[\angle \]A + \[\angle \]C ...\[\left( 1 \right)\]
DF || BC and BD is the transversal,
\[\therefore \] \[\angle \]ADO = \[\angle \]B as they are corresponding angles ...\[\left( 2 \right)\]
In \[\Delta \] ABP, D is the mid point of AB and OD || BP.
\[\therefore \] O is the midpoint of AP from converse of mid point theorem
\[\Rightarrow \] OA = OP
In \[\Delta \] AOD and \[\Delta \] DOP,
OA = OP which is Proved
\[\angle \]AOD = \[\angle \]DOP = \[90{}^\circ \]
 ∠DOP = ∠OPE they are alternate angles & \[\angle \]AOD = \[\angle \]DOP = \[90{}^\circ \] from concept of linear pair
OD = OD since it is common
\[\therefore \] \[\Delta \] AOD congruence \[\Delta \] DOP
We get it from SAS congruence criterion
\[\Rightarrow \] \[\angle \]ADO = \[\angle \]PDO from CECT
\[\Rightarrow \]\[\angle \]PDO = \[\angle \]B from Using \[\left( 2 \right)\]
In quadrilateral PDFE,
\[\angle \]PDO + \[\angle \]PEF = \[\angle \]B + \[\angle \]A + \[\angle \]C = \[\angle \]A + \[\angle \]B + \[\angle \]C from Using \[\left( 1 \right)\]
\[\Rightarrow \]\[\angle \]PDO + \[\angle \]PEF = 180° Since, \[\angle \]A + \[\angle \]B + \[\angle \]C = \[180{}^\circ \]
Hence, quadrilateral PDFE is a cyclic quadrilateral.
Thus, the points E, F, D and P are concyclic.

Note: Student should consider the data given and prove that the quadrilateral PDFE is a cyclic quadrilateral to prove the points E, F, D and P are concyclic for this student should prove all the required similarities of triangles. As A cyclic quadrilateral is a quadrilateral which has all its four vertices lying on a circle. We can prove that the a quadrilateral is cyclic quadrilaterals if opposite angles of the quadrilateral are supplementary.