Question

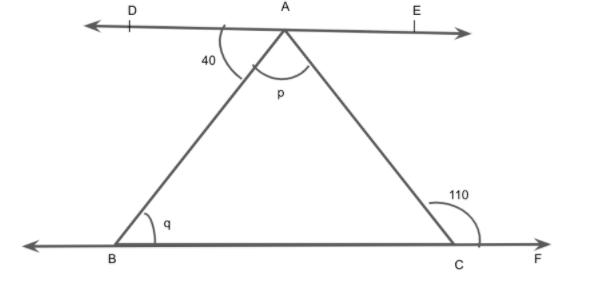
In the figure, \[DE||BC\], \[\angle DAB = 40^\circ \] and \[\angle ACF = 110^\circ \]. Find the value of \[p\] and \[q\].

Answer 1

Hint: First, we will use the angles on one side of a segment are supplementary, so the sum of angles \[\angle ACF\] and \[\angle BCA\] is equal to \[180^\circ \] and then we will use the property that angles on one side of a segment are supplementary, so the sum of angles \[\angle DAB\], \[\angle BAC\] and \[\angle CAE\] is equal to \[180^\circ \]. Then in triangle ABC, we also know that angle sum property tells us that the sum of the three angles are equal to \[180^\circ \].

Complete step-by-step answer:
We are given that \[DE||BC\], \[\angle DAB = 40^\circ \] and \[\angle ACF = 110^\circ \].
We know that the angles on one side of a segment are supplementary, so the sum of angles \[\angle ACF\] and \[\angle BCA\] is equal to \[180^\circ \].
Then, we have
\[ \Rightarrow \angle ACF + \angle BCA{\text{ = 180}}^\circ \]
Substituting the value of the angle \[\angle ACF\] from the diagram in the above equation, we get
\[ \Rightarrow 110^\circ + \angle BCA{\text{ = 180}}^\circ \]
Subtracting the above equation by \[110^\circ \] on both sides, we get
\[
   \Rightarrow 110^\circ + \angle BCA - 110^\circ {\text{ = 180}}^\circ - 110^\circ \\
   \Rightarrow \angle BCA{\text{ = 70}}^\circ \\
 \]
Since, we know that \[\angle BCA = \angle EAC\].
So, we have
\[
   \Rightarrow \angle EAC = \angle BCA \\
   \Rightarrow \angle EAC = 70^\circ \\
 \]
We know that the angles on one side of a segment are supplementary, so the sum of angles \[\angle DAB\], \[\angle BAC\] and \[\angle CAE\] is equal to \[180^\circ \].
Then, we have
\[ \Rightarrow \angle DAB + \angle BAC + \angle CAE{\text{ = 180}}^\circ \]
Substituting the value of the angle \[\angle DAB\] , \[\angle CAE\]and \[\angle BAC\] from the diagram in the above equation, we get
\[
   \Rightarrow 40^\circ + p + 70^\circ {\text{ = 180}}^\circ \\
   \Rightarrow 110^\circ + p{\text{ = 180}}^\circ \\
 \]
Subtracting the above equation by \[110^\circ \] on both sides, we get
\[
   \Rightarrow 110^\circ + p - 110^\circ {\text{ = 180}}^\circ - 110^\circ \\
   \Rightarrow p{\text{ = 70}}^\circ \\
 \]
In triangle ABC, we also know that angle sum property tells us that the sum of the three angles are equal to \[180^\circ \].
Then, we have
\[ \Rightarrow \angle CAB + \angle ABC + \angle BCA{\text{ = 180}}^\circ \]
Substituting the value of the angle \[\angle CAB\] , \[\angle ABC\]and \[\angle BCA\] from the diagram in the above equation, we get
\[
   \Rightarrow q + 70^\circ + 70^\circ {\text{ = 180}}^\circ \\
   \Rightarrow 140^\circ + q{\text{ = 180}}^\circ \\
 \]
Subtracting the above equation by \[140^\circ \] on both sides, we get
\[
   \Rightarrow 140^\circ + q - 140^\circ {\text{ = 180}}^\circ - 140^\circ \\
   \Rightarrow q{\text{ = 40}}^\circ \\
 \]
Hence, the value of \[p\] is \[70^\circ \] and the value of \[q\] is \[40^\circ \].

Note: You need to know the properties of triangles and their mid point. Then we will use the properties accordingly. This is a really simple problem, It is clear from the diagram that it is a triangle. Also, students should always remember that when all the angles are less than 90 degrees, then it is an acute angle and if one of the angles is 90 degrees then the triangle is right angled. The possibility of error in this question can be that you assume the sum is equal to 90 degrees, which is wrong. Also, avoid calculation mistakes.