Question

In the figure, C is a point on the minor arc AB of the circle, with centre O. Given $\angle ACB={{x}^{\circ }}$ and $\angle AOB={{y}^{\circ }}$express $y$ in terms of $x$. Calculate $x$, if ACBO is a parallelogram. \[\]
 

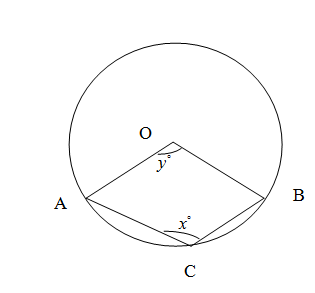
Answer 1

Hint: We use the inscribed angle theorem to conclude that that the central angle formed by the major arc AB at the centre as reflex $\angle AOB$ is twice the inscribed angle $\angle ACB$ to express $y$ in terms of $x$. We use the fact that the opposite angles in parallelogram are equal to find $x$ in the parallelogram ACBO.

Complete step-by-step answer:

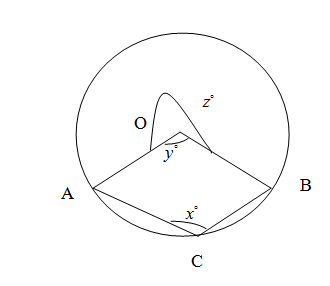
We know that a minor arc is an arc which is smaller than a semicircle and a major arc is the arc larger than the semicircle. We have drawn the figure of circle as given in the question where C is a point in the minor arc of AB and O is the centre.\[\]
We know that the angle subtended by an arc at the centre with radii at the centre is called central angle. The angle subtended at any point on the other (minor if the arc major and major arc if the arc is minor) arc and the chord joining the endpoints of the arc is called inscribed angle the arc. Here in this problem the major arc AB subtends central angle at the centre O with its radii OA, OB as the reflex $\angle AOB$ which whose measure we have denoted in the diagram as ${{z}^{\circ }}.$ So
\[\angle AOB={{z}^{\circ }}\]
Here the major arc AB also subtends inscribed angle on point C on the minor arc AB as $\angle ACB$ with its chords AC, BC whose measurement is given in the question as
\[\angle ACB={{x}^{\circ }}\]
We know from the inscribed angle theorem that the central angle is twice the inscribed angle. So we have,
\[\begin{align}
  & \text{reflex }\angle AOB=2\angle ACB \\
 & \Rightarrow {{z}^{\circ }}=2{{x}^{\circ }} \\
\end{align}\]
We are also given in the question the obtuse$\angle AOB={{y}^{\circ }}$. We see that obtuse $\angle AOB$ and reflex $\angle AOB$ make the complete angle of measure${{360}^{\circ }}$. So we have
\[\begin{align}
  & {{z}^{\circ }}+{{y}^{\circ }}={{360}^{\circ }} \\
 & \Rightarrow {{y}^{\circ }}={{360}^{\circ }}-{{z}^{\circ }} \\
 & \Rightarrow {{y}^{\circ }}={{360}^{\circ }}-2{{x}^{\circ }} \\
\end{align}\]
The expression of $y$ in terms of $x$ is ${{y}^{\circ }}={{360}^{\circ }}-2{{x}^{\circ }}$. We are further asked in the question to calculate $x$ if ACBO is parallelogram. We know that opposite angles in a parallelogram are equal. So we have,
\[\begin{align}
  & \angle ACB=\angle AOB \\
 & \Rightarrow {{x}^{\circ }}={{y}^{\circ }} \\
\end{align}\]
We put previously obtained ${{y}^{\circ }}={{360}^{\circ }}-2{{x}^{\circ }}$ and proceed to get ${{x}^{\circ }}$ as,
\[\begin{align}
  & \Rightarrow {{x}^{\circ }}=360-2{{x}^{\circ }} \\
 & \Rightarrow 3{{x}^{\circ }}={{360}^{\circ }} \\
 & \Rightarrow x={{120}^{\circ }} \\
\end{align}\]

Note: We need to be careful that the major arc subtends the reflex $\angle AOB$ and inscribed $\angle ACB$ while the minor arc subtends obtuse $\angle AOB$ and can inscribe at a point on the major arc AB. The central angle in regular polygon with $n$ sides is the angle at the centre and formed by the line joining centre and two vertices whose measure is $\dfrac{{{360}^{\circ }}}{n}$