Question

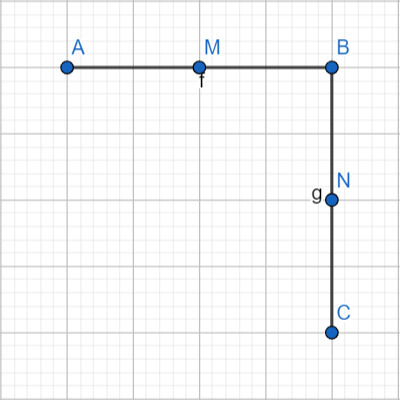
In the figure, BM = BN, M is the midpoint of AB and N is the midpoint of BC. Then the statement AB = BC is

A. True
B. False

Answer 1

Hint: Identify the relation between AB and BM, and also BC and BN. Then accordingly adjust the given condition in the question to find the relation between AB and BC. Thus, comment whether the statement AB = BC is true or false.

Complete step-by-step answer:
It is given that M is the midpoint of AB. Thus, it can be said that the length of BM is half of that of AB.
$\begin{align}
  & \therefore \text{ BM = }\dfrac{\text{AB}}{2}\text{ } \\
 & \Rightarrow \text{ AB = 2BM }....\left( \text{i} \right) \\
\end{align}$
Similarly, N is the midpoint of BC. Thus, the length of BN is half of that of BC.
$\begin{align}
  & \therefore \text{ BN = }\dfrac{\text{BC}}{2}\text{ } \\
 & \Rightarrow \text{BC = 2BN }.....\text{(ii)} \\
\end{align}$
The condition given in the question is BM = BN.
Multiplying both sides of the above equation by 2, we get,
$\begin{align}
  & 2\text{BM = 2BN} \\
 & \therefore \text{ AB }\text{= BC }\left[ \text{from the eqns}\text{. }\left( \text{i} \right)\text{ and }\left( \text{ii} \right) \right] \\
\end{align}$
Thus, it is proved that the statement AB = BC is true.
Hence, the correct answer is option A.

Note: The statement AB = BC would not have been true, if M and N were random points on AB and BC respectively. The two line segments will be equal if and only if the points’ distances from the point B are proportionate to the lengths of AB and BC respectively.